高中物理平抛运动计算题

(8分）如图所示，一架在2000m高空以200m /s的速度水平匀速飞行的轰炸机，要想用两枚炸弹分别轰炸山脚和山顶的敌人碉堡A和B 。已知山脚与山顶的水平距离为1000m，若不计空气阻力，g取10 m / s²，求：

（1）飞机投第一颗炸弹时，飞机离A点的水平距离s₁为多少才能准确击中碉堡A？
（2）当飞机上投弹的时间间隔为9s时，就准确的击中碉堡A和B，则山的高度h为多少？

如图所示，水平传送带的右端与竖直面内的用光滑钢管弯成的“9”形固定轨道相接，钢管内径很小。传送带的运行速度为m/s，将质量kg的可看作质点的滑块无初速地放到传送带端，传送带长度为m，“9”字全高m，“9”字上半部分圆弧半径为m，滑块与传送带间的动摩擦因数为，重力加速g=10m/s²，试求：

（1）滑块从传送带A端运动到B端所需要的时间；
（2）滑块滑到轨道最高点C时对轨道作用力的大小和方向；
（3）若滑块从“9”形轨道D点水平抛出后，恰好垂直撞在倾角的斜面上P点，求P、D两点间的竖直高度 h(保留两位有效数字)。

如图所示，在竖直平面内有一条1/4圆弧形轨道AB，其半径为R=1m，B点的切线方向恰好为水平方向．一个质量为m=lkg的小物体，从轨道顶端A点由静止开始沿轨道下滑，到达轨道末端B点时对轨道的压力为26N，然后做平抛运动，落到地面上的C点，若BC所连直线与水平方向夹角为θ，且tanθ=1.25（不计空气阻力，g=10m/s²），求：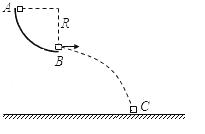

（1）物体在AB轨道上运动时阻力做的功；
（2）物体从B点开始到与BC直线相距最远所用的时间；

(14分)《愤怒的小鸟》是一款时下非常流行的游戏，故事也相当有趣，如图甲，为了报复偷走鸟蛋的肥猪们，鸟儿以自己的身体为武器，如炮弹般弹射出去攻击肥猪们的堡垒。假设小鸟被弹弓沿水平方向弹出，如图乙所示。(取重力加速度g=10m/s²)

(1)若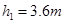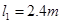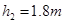，，，要使小鸟飞出去能直接打中肥猪的堡垒，小鸟的初速度应多大?
(2)如果小鸟弹出后，先掉到平台上(此时小鸟距抛出点的水平距离为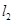)，接触平台瞬间竖直速度变为零，水平速度不变，小鸟在平台上滑行一段距离后，若要打中肥猪的堡垒，小鸟和平台间的动摩擦因数与小鸟弹出时的初速度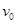之间应满足什么关系(用题中所给的符号、、、、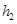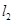g表示)?

如图为某游乐场内水上滑梯轨道示意图，整个轨道在同一竖直平面内，轨道表面粗糙，点A距水面的高度为H， B点距水面的高度为R，一质量为m的游客（视为质点）从A点由静止开始滑下，到B点时沿水平切线方向滑离轨道后落在水面D点， OD=2R，不计空气阻力，重力加速度为g，求：

(1) 游客滑到B点的速度v_B的大小
(2) 游客运动过程中轨道摩擦力对其所做的功W_f

如图所示，半径为r=0.4m的1/4圆形光滑轨道AB固定于竖直平面内，轨道与粗糙的水平地面相切于B点，CDE为固定于竖直平面内的一段内壁光滑的中空方形细管，DE段被弯成以O为圆心、半径R=0.2m的一小段圆弧，管的C端弯成与地面平滑相接，O点位于地面，OE连线竖直．可视为质点的物块b，从A点由静止开始沿轨道下滑，经地面进入细管（b横截面略小于管中空部分的横截面），b滑到E点时受到细管下壁的支持力大小等于所受重力的1/2．已知物块b的质量m = 0.4kg，g取10m/s²．

（1）求物块b滑过E点时的速度大小v_E．
（2）求物块b滑过地面BC过程中克服摩擦力做的功W_f．
（3）若将物块b静止放在B点，让另一可视为质点的物块a，从A点由静止开始沿轨道下滑，滑到B点时与b发生弹性正碰，已知a的质量M≥m，求物块b滑过E点后在地面的首次落点到O点的距离范围．

如图所示，倾角为θ=45°的粗糙平直导轨与半径为R的光滑圆环轨道相切，切点为B，整个轨道处在竖直平面内。一质量为m的小滑块从导轨上离地面高为h=3R的D处无初速下滑进入圆环轨道.接着小滑块从圆环最高点C水平飞出，恰好击中导轨上与圆心O等高的P点，不计空气阻力. 求：

（1）滑块运动到圆环最高点C时的速度的大小；
（2）滑块运动到圆环最低点时对圆环轨道压力的大小；
（3）滑块在斜面轨道BD间运动的过程中克服摩擦力做的功。

如图所示，长为L的细绳上端系一质量不计的环，环套在光滑水平杆上，在细绳的下端吊一个质量为m的铁球(可视作质点)，球离地的高度h＝L．现让环与球一起以v＝的速度向右运动，在A处环被挡住而立即停止，已知A离右墙的水平距离也为L，当地的重力加速度为g，不计空气阻力．求：

(1)在环被挡住而立即停止时绳对小球的拉力大小；
(2)若在环被挡住后，细绳突然断裂，则在以后的运动过程中，球的第一次碰撞点离墙角B点的距离是多少？

如图所示，在同一竖直平面内，一轻质弹簧一端固定，另一自由端恰好与水平线AB平齐，静止放于倾角为60°的光滑斜面上。一长为L＝10cm的轻质细绳一端固定在O点，另一端系一质量为m＝1 kg的小球，将细绳拉至水平，使小球在位置C由静止释放，小球到达最低点D时，细绳刚好被拉断。之后小球在运动过程中恰好沿斜面方向将劲度系数为k=100N/m的弹簧压缩，已知弹簧的弹性势能E_P与弹簧的劲度系数k及弹簧的形变量x的关系式为。g＝10 m/s²，求：

(1) 当弹簧的形变量为x=9cm时小球的加速度大小；
(2) D点到水平线AB的高度h；
(3) 在小球的运动过程中，小球的动能最大值。

在同一高度，以大小相等的速度抛出三个小球，A球竖直上抛，B球竖直下抛，C球平抛，在空中飞行时间最长的为6s，飞行时间最短的为2s，求另一小球的飞行时间及C球飞行的水平距离。g=10

如图所示，半径R＝0.4 m的光滑圆弧轨道BC固定在竖直平面内，轨道的上端点B和圆心O的连线与水平方向的夹角θ＝30°，下端点C为轨道的最低点且与粗糙水平面相切，一根轻质弹簧的右端固定在竖直挡板上．质量m＝0.1  kg的小物块(可视为质点)从空中A点以v₀＝2 m/s的速度被水平抛出，恰好从B点沿轨道切线方向进入轨道，经过C点后沿水平面向右运动至D点时，弹簧被压缩至最短，C、D两点间的水平距离L＝1.2 m，小物块与水平面间的动摩擦因数μ＝0.5，g取10  m/s².求：

(1)小物块经过圆弧轨道上B点时速度v_B的大小；
(2)小物块经过圆弧轨道上C点时对轨道的压力大小；
(3)弹簧的弹性势能的最大值E_pm.

如图所示，质量为m的小球沿光滑的水平面冲上一光滑的半圆形轨道，轨道半径为R，小球在轨道最高点对轨道压力等于0.5mg，重力加速度为g，求：

（1）小球在最高点的速度大小；
（2）小球落地时，距最高点的水平位移大小；
（3）小球经过半圆轨道最低点时，对轨道的压力．

如图，BC为半径等于Ｒ＝竖直放置的光滑细圆管，O为细圆管的圆心，BO与竖直线的夹角为45°；在圆管的末端C连接一光滑水平面，水平面上一质量为Ｍ＝1.5kg的木块与一轻质弹簧拴接，轻弹簧的另一端固定于竖直墙壁上．现有一质量为m=0.5kg的小球从Ｏ点正上方某处Ａ点以v₀水平抛出，恰好能垂直OB从B点进入细圆管，小球从进入圆管开始即受到始终竖直向上的力F=5N的作用，当小球运动到圆管的末端C时作用力F立即消失．小球过后与木块发生完全非弹性碰撞（g=10m/s²）．求：

（1）小球在Ａ点水平抛出的初速度v₀；
（2）在圆管运动中圆管对小球的支持力Ｎ；
（3）弹簧的最大弹性势能Ｅ_Ｐ．

如图所示，某工厂传送带装置倾斜放置，倾角=37^o，传送带AB长度x_o=l0m。有一水平平台CD高度保持6.45m不变。现调整D端位置，当D、B的水平距离合适时，自D端水平抛出的物体恰好从B点沿BA方向冲上斜面，此后D端固定不动，g=l0m/s²。另外，传送带B端上方安装一极短的小平面，与传送带AB平行共面，保证自下而上传送的物体能沿AB方向由B点斜向上抛出。（sin37^o=0．6，cos37^o=0．8）

（1）求D、B的水平距离；
（2）若传送带以5m/s的速度逆时针匀速运行，某物体甲与传送带间动摩擦因数μ₁＝0.9，自A点沿传送带方向以某一初速度冲上传送带时，恰能水平落到水平台的D端，求物体甲的最大初速度v_o1。
（3）若传送带逆时针匀速运行，某物体乙与传送带间动摩擦因数μ₂＝0.6，自A点以v_o2=11m/s的初速度沿传送带方向冲上传送带时，恰能水平落到水平台的D端，求传送带的速度v′。

如图所示，一质量为M＝5.0kg，长度L=4m的平板车静止在水平地面上，距离平板车右侧S=16.5m处有一固定障碍物．障碍物上固定有一电动机A。另一质量为m＝2.0kg可视为质点的滑块，以v₀＝8m/s的水平初速度从左端滑上平板车，同时电动机A对平板车施加一水平向右、大小为22.5N的恒力F．1s后电动机A突然将功率变为P=52.5w并保持不变，直到平板车碰到障碍物停止运动时，电动机A也同时关闭。滑块沿水平飞离平板车后，恰能无碰撞地沿圆弧切线从B点滑入光滑竖直圆弧轨道，并沿轨道下滑．已知平板车间与滑块的动摩擦因数μ₁＝0.5，平板车与地面的动摩擦因数μ₂＝0.25，圆弧半径为R＝1.0m，圆弧所对的圆心角∠BOD＝θ＝106⁰，g取10m/s²，sin53°＝0.8，cos53°＝0.6，不计空气阻力，求：

（1）0 1s时间内，滑块相对小车运动的位移x；
（2）电动机A做功W；
（3）滑块运动到圆弧轨道最低点C时对轨道压力的大小F_N．