下面结论中,正确命题的个数为_____________.
①当直线l1和l2斜率都存在时,一定有k1=k2⇒l1∥l2.
②如果两条直线l1与l2垂直,则它们的斜率之积一定等于-1.
③已知直线l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0(A1、B1、C1、A2、B2、C2为常数),若直线l1⊥l2,则A1A2+B1B2=0.
④点P(x0,y0)到直线y=kx+b的距离为 .
.
⑤直线外一点与直线上一点的距离的最小值就是点到直线的距离.
⑥若点A,B关于直线l:y=kx+b(k≠0)对称,则直线AB的斜率等于 ,且线段AB的中点在直线l上.
,且线段AB的中点在直线l上.
已知函数 .若
.若 的图像向左平移
的图像向左平移 个单位所得的图像与
个单位所得的图像与 的图像重合,则
的图像重合,则 的最小值为____.
的最小值为____.
某校选修乒乓球课程的学生中,高一年级有30名,高二年级有40名.现用分层抽样的方法在
这70名学生中抽取一个样本,已知在高一年级的学生中抽取了9名,则在高二年级的学生中应抽取的人数
为 .
埃及数学中有一个独特现象:除 用一个单独的符号表示以外,其它分数都要写成若干个单分数和的形式.例如
用一个单独的符号表示以外,其它分数都要写成若干个单分数和的形式.例如 ,可以这样理解:假定有两个面包,要平均分给5个人,如果每人
,可以这样理解:假定有两个面包,要平均分给5个人,如果每人 ,不够,每人
,不够,每人 ,余
,余 ,再将这
,再将这 分成5份,每人得
分成5份,每人得 ,这样每人分得
,这样每人分得 .形如
.形如 的分数的分解:
的分数的分解: ,
, ,
, ,按此规律,
,按此规律, ;
;
 .
.
已知函数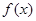 的定义域为
的定义域为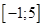 ,部分对应值如表,
,部分对应值如表,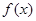 的导函数
的导函数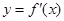 的图象如图所示,
的图象如图所示,
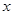 |
-1 |
0 |
4 |
5 |
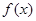 |
1 |
2 |
2 |
1 |
下列关于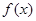 的命题:
的命题:
①函数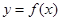 是周期函数;
是周期函数;
②函数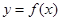 在
在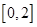 上减函数;
上减函数;
③如果当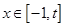 时,
时,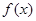 的最大值是2,那么
的最大值是2,那么 的最大值是4;
的最大值是4;
④当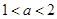 时,函数
时,函数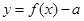 有4个零点;
有4个零点;
⑤ 函数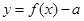 的零点个数可能为0,1,2,3,4.
的零点个数可能为0,1,2,3,4.
其中正确命题的序号是________(写出所有正确命题的序号).
如图,已知边长为4的正方形ABCD,E是BC边上一动点(与B、C不重合),连结AE,作EF⊥AE交∠BCD的外角平分线于F.设 ,记
,记 ,则函数
,则函数 的值域是 ;当
的值域是 ;当 面积最大时,
面积最大时, .
.
