已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆C上的点到焦点距离的最大值为3,最小值为1.
(1)求椭圆C的标准方程
(2)若直线L:y=kx+m与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点D.求证:直线L过定点,并求处该定点的坐标。
(本小题满分13分)已知函数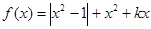 .
.
(1)若对于区间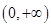 内的任意
内的任意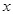 ,总有
,总有 成立,求实数
成立,求实数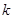 的取值范围;
的取值范围;
(2)若函数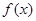 在区间
在区间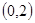 内有两个不同的零点
内有两个不同的零点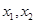 ,求:
,求:
①实数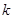 的取值范围; ②
的取值范围; ②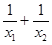 的取值范围.
的取值范围.
学习雷锋精神前半年内某单位餐厅的固定餐椅经常有损坏,学习雷锋精神时全修好;单位对学习雷锋精神前后各半年内餐椅的损坏情况作了一个大致统计,具体数据如下:
| |
损坏餐椅数 |
未损坏餐椅数 |
总 计 |
| 学习雷锋精神前 |
50 |
150 |
200 |
| 学习雷锋精神后 |
30 |
170 |
200 |
| 总 计 |
80 |
320 |
400 |
(Ⅰ)求:学习雷锋精神前后餐椅损坏的百分比分别是多少?
并初步判断损毁餐椅数量与学习雷锋精神是否有关?
(Ⅱ)请说明是否有97.5%以上的把握认为损毁餐椅数量与学习雷锋精神有关?
参考公式: ,
,
| P(K2≥k0) |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| k0 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(本小题满分15分)已知数列 是公差不为零的等差数列,
是公差不为零的等差数列, ,且
,且 成等比数列.
成等比数列.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设数列 满足:
满足: ,
, ,令
,令 ,
, ,求数列
,求数列 的前
的前 项和
项和 .
.
(本题14分)已知函数 ,其中
,其中
(Ⅰ)若函数 、
、 存在相同的零点,求
存在相同的零点,求 的值;
的值;
(Ⅱ)若存在两个正整数 、
、 ,当
,当 时,有
时,有 与
与 同时成立,求
同时成立,求 的最大值及
的最大值及 取最大值时
取最大值时 的取值范围.
的取值范围.
已知数列 满足:
满足: ,
, .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)(ⅰ)证明:当 时,
时, ;
;
(ⅱ)若正整数 满足
满足 ,求
,求 的值.
的值.
(本小题满分15分)已知数列 中,
中, (实数
(实数 为常数),
为常数),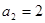 ,
,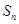 是其前
是其前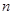 项和,且
项和,且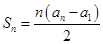 .数列
.数列 是等比数列,
是等比数列, ,
,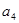 恰为
恰为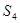 与
与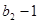 的等比中项.
的等比中项.
(Ⅰ)证明:数列 是等差数列;
是等差数列;
(Ⅱ)求数列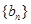 的通项公式;
的通项公式;
(Ⅲ)若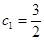 ,当
,当 时
时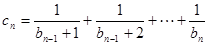 ,
,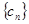 的前
的前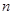 项和为
项和为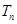 ,求证:对任意
,求证:对任意 ,都有
,都有 .
.
如图,已知 为抛物线
为抛物线 的焦点,点
的焦点,点 在该抛物线上,其中
在该抛物线上,其中 关于
关于 轴对称(
轴对称( 在第一象限),且直线
在第一象限),且直线 经过点
经过点 .
.
(Ⅰ)若 的重心为
的重心为 ,求直线
,求直线 的方程;
的方程;
(Ⅱ)设 ,其中
,其中 为坐标原点,求
为坐标原点,求 的最小值.
的最小值.
已知 为实数,且
为实数,且 ,数列
,数列 的前
的前 项和
项和 满足
满足
(Ⅰ)求证:数列 为等比数列,并求出公比
为等比数列,并求出公比 ;
;
(Ⅱ)若 对任意正整数
对任意正整数 成立,求证:当
成立,求证:当 取到最小整数时,对于
取到最小整数时,对于 都有
都有 .
.
已知横坐标为 的点
的点 在曲线
在曲线 :
: 上,曲线
上,曲线 在点
在点 处的切线与直线
处的切线与直线 交于点
交于点 ,与
,与 轴交于点
轴交于点 .设点
.设点 ,
, 的横坐标分别为
的横坐标分别为 ,记
,记 .正数数列
.正数数列 满足
满足 ,
, .
.
(Ⅰ)写出 之间的关系式;
之间的关系式;
(Ⅱ)若数列 为递减数列,求实数
为递减数列,求实数 的取值范围;
的取值范围;
(Ⅲ)若 ,设数列
,设数列 的前
的前 项和为
项和为 ,求证:
,求证: .
.
已知椭圆 :
: 上的点到左焦点的最大距离是
上的点到左焦点的最大距离是 ,且点
,且点 在椭圆
在椭圆 上,其中
上,其中 为椭圆
为椭圆 的离心率.
的离心率.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)如图所示, 是椭圆
是椭圆 上的两点,且
上的两点,且 ,求
,求 面积的取值范围.
面积的取值范围.
已知中心在原点,焦点在坐标轴上的椭圆 的方程为
的方程为 它的离心率为
它的离心率为 ,一个焦点是
,一个焦点是 ,过直线
,过直线 上一点引椭圆
上一点引椭圆 的两条切线,切点分别是A、B.
的两条切线,切点分别是A、B.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)若在椭圆
 上的点
上的点 处的切线方程是
处的切线方程是 .求证:直线AB恒过定点,并求出定点的坐标;
.求证:直线AB恒过定点,并求出定点的坐标;
(Ⅲ)记点C为(Ⅱ)中直线AB恒过的定点,问否存在实数 ,使得
,使得 成立,若成立求出
成立,若成立求出 的值,若不存在,请说明理由
的值,若不存在,请说明理由