已知中心在原点，焦点在坐标轴上的椭圆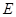
的方程为
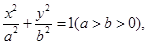它的离心率为
，一个焦点是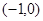
，过直线
上一点引椭圆的两条切线，切点分别是A、B．
（Ⅰ）求椭圆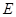的方程；
（Ⅱ）若在椭圆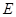
上的点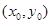
处的切线方程是
．求证：直线AB恒过定点，并求出定点的坐标；
（Ⅲ）记点C为（Ⅱ）中直线AB恒过的定点，问否存在实数
，使得
成立，若成立求出的值，若不存在，请说明理由
相关试题
．
经过点
，且在两坐标轴上的截距相等，求直线
经过点
满足：
．
，求数列
的前
项和
．
为
个正数
的“均倒数”．已知数列
的前
，
，试判断并说明数列
的单调性；
的前n项和
．
时，求
的值；
，已知在
中，三个内角A、B、C所对的边分别是
，若
，设
，求
的取值范围．
分别是
三内角A、B、C所对的边，
中，
，设数列
的前
项和为
，求证：
．推荐套卷
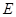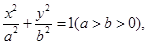已知中心在原点，焦点在坐标轴上的椭圆的方程为它的离心率为，一个焦点是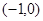，过直线上一点引椭圆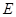的两条切线，切点分别是A、B．
（Ⅰ）求椭圆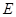的方程；
（Ⅱ）若在椭圆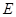上的点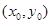处的切线方程是．求证：直线AB恒过定点，并求出定点的坐标；
（Ⅲ）记点C为（Ⅱ）中直线AB恒过的定点，问否存在实数，使得 成立，若成立求出的值，若不存在，请说明理由
粤公网安备 44130202000953号