高中数学解答题

（本题15分）已知函数是定义在上的偶函数，且当时， ．
（1）写出函数的解析式；
（2）写出函数的增区间；
（3）若函数，求函数的最小值.[来

（本题14分）某公司生产一种电子仪器的固定成本为20 000元，每生产一台仪器需增加投入100元，已知总收益满足函数：
（其中x是仪器的月产量）．
(1)将利润表示为月产量的函数f(x)；
(2)当月产量为何值时，公司所获利润最大？最大利润为多少元？(总收益＝总成本＋利润)

（本题18分）已知函数，
（1）画出函数图像；
（2）求，的值；
（3）当时，求取值的集合.

（本题18分）某租赁公司拥有汽车100辆，当每辆车的月租金为3000元时，可全部租出。当每辆车的月租金每增加50元时，未租出的车将会增加一辆。租出的车每辆每月需要维护费150元，未租出的车每辆每月需要维护费50元。
（1）当每辆车的月租金定为3600元时，能租出多少辆车？
（2）当每辆车的月租金定为多少元时，租赁公司的月收益最大？最大月收益是多少？

（本小题满分14分）在△中，内角的对边分别为，已知
（Ⅰ）求的值；
（Ⅱ）的值．

（本小题满分14分）记等比数列的前n项和为，已知，，求的通项公式。

（本小题满分12分）已知集合，．
（1）当时，求集合，；   
（2）若，求实数m的取值范围．

（本小题满分12分）某服装厂生产一种服装，每件服装的成本为40元，出厂单价定为60元．该厂为鼓励销售商订购，决定当一次订购量超过100件时，每多订购一件，订购的全部服装的出厂单价就降低0．02元．根据市场调查，销售商一次订购量不会超过500件．
（1）设一次订购量为x件，服装的实际出厂单价为P元，写出函数P=f（x）的表达式；
（2）当销售商一次订购了450件服装时，该服装厂获得的利润是多少元？
（服装厂售出一件服装的利润=实际出厂单价-成本）

（本小题满分12分）已知函数是定义在上的奇函数，且，
（1）确定函数的解析式；
（2）用定义证明在上是增函数；
（3）解不等式．

设正整数构成的数列{a_n}使得a_10k﹣9+a_10k﹣8+…+a_10k≤19对一切k∈N^*恒成立．记该数列若干连续项的和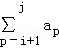为S（i，j），其中i，j∈N^*，且i＜j．求证：所有S（i，j）构成的集合等于N^*．

设a，b，c为正数，利用排序不等式证明a³+b³+c³≥3abc．

设a，b，c是正实数，求证：a^ab^bc^c≥（abc）．

设a₁，a₂，…，a_n为正数，求证：++…++≥a₁+a₂+…+a_n．

若a₁≤a₂≤…≤a_n，而b₁≥b₂≥…≥b_n或a₁≥a₂≥…≥a_n而b₁≤b₂≤…≤b_n，证明：≤（）•（）．当且仅当a₁=a₂=…=a_n或b₁=b₂=…=b_n时等号成立．

设a₁，a₂，…，a_n为实数，证明：≤．