某商品定价为每件60元,不加收附加税时每年大约销售80万件,若政府征收附加税,每销售100元要征收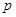 元(即税率为
元(即税率为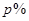 ),因此每年销量将减少
),因此每年销量将减少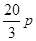 万件.
万件.
(1)将政府每年对该商品征收的总税金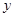 (万元),表示成
(万元),表示成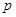 的函数,并指出这个函数的定义域;
的函数,并指出这个函数的定义域;
(2)要使政府在此项经营中每年收取的税金不少于128万元,问税率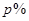 应怎样确定?
应怎样确定?
已知函数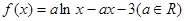 .
.
(1)求函数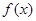 的单调区间;
的单调区间;
(2)函数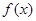 的图象在
的图象在 处切线的斜率为
处切线的斜率为 若函数
若函数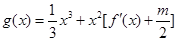 在区间(1,3)上不是单调函数,求m的取值范围.
在区间(1,3)上不是单调函数,求m的取值范围.
已知函数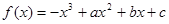 图像上的点
图像上的点 处的切线方程为
处的切线方程为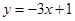 .
.
(1)若函数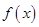 在
在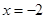 时有极值,求
时有极值,求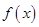 的表达式;
的表达式;
(2)函数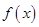 在区间
在区间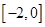 上单调递增,求实数
上单调递增,求实数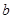 的取值范围.
的取值范围.
已知 展开式中的倒数第三项的系数为45,求:
展开式中的倒数第三项的系数为45,求:
(1)含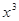 的项;
的项;
(2)系数最大的项.
(本小题满分10分)
已知数列 ,其前
,其前 项和为
项和为 .
.
(Ⅰ)求 ,
, ;
;
(Ⅱ)求数列 的通项公式,并证明数列
的通项公式,并证明数列 是等差数列;
是等差数列;
(Ⅲ)如果数列 满足
满足 ,请证明数列
,请证明数列 是等比数列,并求其前
是等比数列,并求其前 项和
项和 .
.
(本小题满分8分)
某市居民1999~2003年货币收入 与购买商品支出
与购买商品支出 的统计资料如下表所示:
的统计资料如下表所示:
单位:亿元
| 年份 |
1999 |
2000 |
2001 |
2002 |
2003 |
货币收入 |
40 |
42 |
44 |
47 |
50 |
购买商品支出 |
33 |
34 |
36 |
39 |
41 |
(Ⅰ)画出散点图,判断x与Y是否具有相关关系;
(Ⅱ)已知 ,请写出Y对x的回归直线方程,并估计货币收入为52(亿元)时,购买商品支出大致为多少亿元?
,请写出Y对x的回归直线方程,并估计货币收入为52(亿元)时,购买商品支出大致为多少亿元?
在直角坐标平面内,以坐标原点 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系. 已知点
轴的非负半轴为极轴建立极坐标系. 已知点 、
、 的极坐标分别为
的极坐标分别为 、
、 ,曲线
,曲线 的参数方程为
的参数方程为 为参数).
为参数).
(Ⅰ)求直线 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若直线 和曲线C只有一个交点,求
和曲线C只有一个交点,求 的值.
的值.
设数列 的前
的前 项和为
项和为 ,且满足
,且满足
 .
.
(Ⅰ)求证:数列 为等比数列;
为等比数列;
(Ⅱ)求通项公式 ;
;
(Ⅲ)若数列 是首项为1,公差为2的等差数列,求数列
是首项为1,公差为2的等差数列,求数列 的前
的前 项和为
项和为 .
.
在 中,角
中,角 ,
, ,
, 所对的边长分别是
所对的边长分别是 ,
, ,
, . 满足
. 满足 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)求 的最大值.
的最大值.
申请某种许可证,根据规定需要通过统一考试才能获得,且考试最多允许考四次. 设 表示一位申请者经过考试的次数,据统计数据分析知
表示一位申请者经过考试的次数,据统计数据分析知 的概率分布如下:
的概率分布如下:
 |
1 |
2 |
3 |
4 |
| P |
0.1 |
 |
0.3 |
0.1 |
(Ⅰ)求一位申请者所经过的平均考试次数;
(Ⅱ)已知每名申请者参加 次考试需缴纳费用
次考试需缴纳费用 (单位:元),求两位申请者所需费用的和小于500元的概率;
(单位:元),求两位申请者所需费用的和小于500元的概率;
(Ⅲ)在(Ⅱ)的条件下, 4位申请者中获得许可证的考试费用低于300元的人数记为 ,求
,求 的分布列.
的分布列.