已知 a∈ R,若 a-1+( a-2) i( i为虚数单位)是实数,则 a=( )
| A. |
1 |
B. |
-1 |
C. |
2 |
D. |
-2 |
2020年3月14日是全球首个国际圆周率日(
Day).历史上,求圆周率
的方法有多种,与中国传统数学中的"割圆术"相似.数学家阿尔·卡西的方法是:当正整数
充分大时,计算单位圆的内接正 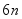 边形的周长和外切正
边形的周长和外切正 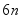 边形(各边均与圆相切的正
边形(各边均与圆相切的正 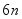 边形)的周长,将它们的算术平均数作为
的近似值.按照阿尔·卡西的方法,
的近似值的表达式是( ).
边形)的周长,将它们的算术平均数作为
的近似值.按照阿尔·卡西的方法,
的近似值的表达式是( ).
| A. |
|
B. |
|
| C. |
|
D. |
|
在等差数列 中, , .记 ,则数列 ( ).
| A. |
有最大项,有最小项 |
B. |
有最大项,无最小项 |
| C. |
无最大项,有最小项 |
D. |
无最大项,无最小项 |
设 是双曲线 的两个焦点, 为坐标原点,点 在 上且 ,则 的面积为( )
| A. |
|
B. |
3 |
C. |
|
D. |
2 |
设函数 在 的图像大致如下图,则 f( x)的最小正周期为( )

| A. |
|
B. |
|
| C. |
|
D. |
|
已知△ ABC是面积为 的等边三角形,且其顶点都在球 O的球面上.若球 O的表面积为16 π,则 O到平面 ABC的距离为( )
| A. |
|
B. |
|
C. |
1 |
D. |
|
设 为坐标原点,直线 与双曲线 的两条渐近线分别交于 两点,若 的面积为8,则 的焦距的最小值为( )
| A. |
4 |
B. |
8 |
C. |
16 |
D. |
32 |
若过点(2,1)的圆与两坐标轴都相切,则圆心到直线 的距离为( )
| A. |
|
B. |
|
C. |
|
D. |
|
已知函数 f( x)=sin x+ ,则( )
| A. |
f(x)的最小值为2 |
B. |
f(x)的图像关于y轴对称 |
| C. |
f(x)的图像关于直线 对称 |
D. |
f(x)的图像关于直线 对称 |
在平面内, A, B是两个定点, C是动点,若 ,则点 C的轨迹为( )
| A. |
圆 |
B. |
椭圆 |
C. |
抛物线 |
D. |
直线 |