2020年3月14日是全球首个国际圆周率日(
Day).历史上,求圆周率
的方法有多种,与中国传统数学中的"割圆术"相似.数学家阿尔·卡西的方法是:当正整数
充分大时,计算单位圆的内接正 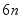 边形的周长和外切正
边形的周长和外切正  边形(各边均与圆相切的正
边形(各边均与圆相切的正  边形)的周长,将它们的算术平均数作为
的近似值.按照阿尔·卡西的方法,
的近似值的表达式是( ).
边形)的周长,将它们的算术平均数作为
的近似值.按照阿尔·卡西的方法,
的近似值的表达式是( ).
| A. |
|
B. |
|
| C. |
|
D. |
|
推荐套卷
2020年3月14日是全球首个国际圆周率日(
Day).历史上,求圆周率
的方法有多种,与中国传统数学中的"割圆术"相似.数学家阿尔·卡西的方法是:当正整数
充分大时,计算单位圆的内接正 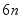 边形的周长和外切正
边形的周长和外切正  边形(各边均与圆相切的正
边形(各边均与圆相切的正  边形)的周长,将它们的算术平均数作为
的近似值.按照阿尔·卡西的方法,
的近似值的表达式是( ).
边形)的周长,将它们的算术平均数作为
的近似值.按照阿尔·卡西的方法,
的近似值的表达式是( ).
| A. |
|
B. |
|
| C. |
|
D. |
|