已知函数 ,其中
,其中 .
.
(1)求函数 的单调区间;
的单调区间;
(2)若直线 是曲线
是曲线 的切线,求实数
的切线,求实数 的值;
的值;
(3)设 ,求
,求 在区间
在区间 上的最大值.(其中
上的最大值.(其中 为自然对数的底数)
为自然对数的底数)
已知函数 .
.
(Ⅰ)若 ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)若函数 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数 的取值范围;
的取值范围;
(Ⅲ)若 ,且至少存在一点
,且至少存在一点 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
设函数
(I) 讨论 的单调性;
的单调性;
(II)若 有两个极值点
有两个极值点 和
和 ,记过点
,记过点 的直线的斜率为
的直线的斜率为 ,问:是否存在
,问:是否存在 ,使得
,使得 ?若存在,求出
?若存在,求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
参考答案
已知函数 的图象在与
的图象在与 轴交点处的切线方程是
轴交点处的切线方程是 .
.
(I)求函数 的解析式;
的解析式;
(II)设函数 ,若
,若 的极值存在,求实数
的极值存在,求实数 的取值范围以及函数
的取值范围以及函数 取得极值时对应的自变量
取得极值时对应的自变量 的值.
的值.
(本小题满分14分)已知函数 .
.
(Ⅰ)若曲线 在
在 和
和 处的切线互相平行,求
处的切线互相平行,求 的值;
的值;
(Ⅱ)求 的单调区间;
的单调区间;
(Ⅲ)设 ,若对任意
,若对任意 ,均存在
,均存在 ,使得
,使得 ,求
,求 的取值范围.
的取值范围.
(本题共10分)已知函数 。
。
(Ⅰ)若曲线 在
在 处的切线与直线
处的切线与直线 垂直,求
垂直,求 的值;
的值;
(Ⅱ)若函数 在区间(
在区间( ,
, )内是增函数,求
)内是增函数,求 的取值范围。
的取值范围。
已知函数
 ).
).
(Ⅰ) 若 ,试确定函数
,试确定函数 的单调区间;
的单调区间;
(Ⅱ) 若函数 在其图象上任意一点
在其图象上任意一点 处切线的斜率都小于
处切线的斜率都小于 ,求实数
,求实数 的取值范围.
的取值范围.
(本小题满分12分)
设二次函数 ,函数
,函数 ,且有
,且有 ,
,
(1)求函数 的解析式;
的解析式;
(2)是否存在实数k和p,使得 成立,若存在,求出k和p的值;若不存在,说明理由.
成立,若存在,求出k和p的值;若不存在,说明理由.
已知函数 ,其中
,其中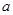 为实数.
为实数.
(Ⅰ)当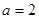 时,求曲线
时,求曲线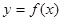 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)是否存在实数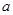 ,使得对任意
,使得对任意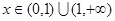 ,
, 恒成立?若不存在,请说明理由,若存在,求出
恒成立?若不存在,请说明理由,若存在,求出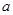 的值并加以证明.
的值并加以证明.
(文)已知 在
在 处有极值,其图象在
处有极值,其图象在 处的切线与直线
处的切线与直线 平行.
平行.
(1)求函数的单调区间;
(2)若 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。