高中数学组合几何试题

设曲线在点（1，1）处的切线与x轴的交点的横坐标为,令，则的值为                .

函数单调增区间是          ;

曲线在点处的切线方程是          ;

已知，则         ；

曲线在点（1，）处的切线方程为（    ）

A．	B．
C．	D．

若对任意实数x，有¦(―x)=―¦(x)，g(―x)=g(x)，且x>0时¦′ (x)>0，g′ (x)>0，则x<0时

A．¦′(x)>0，g′ (x)>0	B．¦′(x)>0，g′ (x)<0
C．¦′(x)<0，g′ (x)>0	D．¦′(x)<0，g′ (x)<0

设，函数的导函数是，且是奇函数，若曲线y = f(x)的某一切线斜率是，则切点的横坐标是（   ）

A．ln2

B．–ln2

C．

D．

函数的单调增区间为        ．

已知函数 $f\left(x\right)=\frac{\ln x+k}{e^x}$为常数， $e$=2.71828…是自然对数的底数)，曲线 $y=f\left(x\right)$在点 $\left(1,f\left(1\right)\right)$处的切线与 $x$轴平行.
(Ⅰ)求 $k$的值；
(Ⅱ)求 $f\left(x\right)$的单调区间；
(Ⅲ)设 $g\left(x\right)=xf\left(x\right)$，其中 $f^{`}\left(x\right)$为 $f\left(x\right)$的导函数.证明：对任意 $x>0,g\left(x\right)<1+e^{-2}$.

已知函数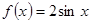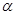（为常数），则（      ）

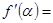A．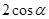

B．0

C．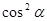

D．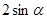

已知函数，若的单调减区间是（0，4），则在曲线的切线中，斜率最小的切线方程是___________

函数在点处的切线与函数围成的图形的面积等于                       。

已知函数 $f\left(x\right)=\frac{\ln x+k}{e^x}$（ $k$为常数， $e=2.71828...$是自然对数的底数），曲线 $y=f\left(x\right)$在点 $(1,f(1\left)\right)$处的切线与 $x$轴平行.
（Ⅰ）求 $k$的值；
（Ⅱ）求 $f\left(x\right)$的单调区间；
（Ⅲ）设 $g\left(x\right)=(x^2+x)f`\left(x\right)$,其中 $f`\left(x\right)$为 $f\left(x\right)$的导函数.证明：对任意 $x>0,g\left(x\right)<1+e^{-2}$.

函数，若，则       .

若函数f(x)＝lnx－ax²－2x存在单调递减区间，实数a的取值范围是