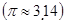如图,在三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
(1)证明:AB⊥A1C;
(2)若AB=CB=2,A1C= ,求三棱柱ABC-A1B1C1的体积;
,求三棱柱ABC-A1B1C1的体积;
(3)若平面ABC⊥平面AA1B1B,AB=CB=2,求直线A1C与平面BB1C1C所成角的正弦值.
如图是某三棱柱被削去一个底面后的直观图与侧(左)视图、俯视图.已知CF=2AD,侧(左)视图是边长为2的等边三角形;俯视图是直角梯形,有关数据如图所示.求该几何体的体积.
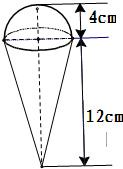
如图所示是一几何体的直观图、正(主)视图、侧(左)视图、俯视图.
(1)若F为PD的中点,求证:AF⊥面PCD;
(2)求几何体BEC-APD的体积.
已知四棱锥PABCD的底面ABCD是边长为2的正方形,PD⊥底面ABCD,E,F分别为棱BC,AD的中点.
(1)求证:DE∥平面PFB;
(2)已知二面角PBFC的余弦值为 ,求四棱锥PABCD的体积.
,求四棱锥PABCD的体积.
已知一个四棱锥P-ABCD的三视图(正视图与侧视图为直角三角形,俯视图是带有一条对角线的正方形)如图,E是侧棱PC的中点.
(1)求四棱锥P-ABCD的体积;
(2)求证:平面APC⊥平面BDE.
下图是一几何体的直观图、主视图、俯视图、左视图.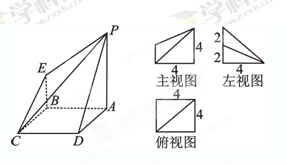
(1)若 为
为 的中点,求证:
的中点,求证: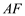
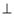 面
面 ;
;
(2)证明 面
面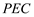 .
.
(3)求该几何体的体积.
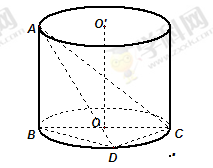
如图,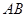 是圆柱体
是圆柱体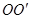 的一条母线,
的一条母线,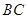 过底面圆的圆心
过底面圆的圆心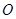 ,
,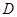 是圆
是圆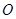 上不与点
上不与点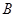 、
、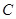 重合的任意一点,已知棱
重合的任意一点,已知棱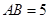 ,
,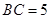 ,
,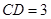 .
.
(1)求证: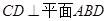 ;
;
(2)将四面体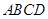 绕母线
绕母线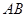 转动一周,求
转动一周,求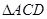 的三边在旋转过程中所围成的几何体的体积.
的三边在旋转过程中所围成的几何体的体积.
在斜三棱柱 中,侧面
中,侧面 平面
平面 ,
, ,
, 为
为 中点.
中点.
(1)求证: ;
;
(2)求证: 平面
平面 ;
;
(3)若 ,
, ,求三棱锥
,求三棱锥 的体积.
的体积.
请您设计一个帐篷,它下部的形状是高为1m正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如图所示)。试问当帐篷的顶点O到底面中心O1的距离为多少时,帐篷的体积最大?
如图,储油灌的表面积 为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.
为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.
⑴试用半径 表示出储油灌的容积
表示出储油灌的容积 ,并写出
,并写出 的范围.
的范围.
⑵当圆柱高 与半径
与半径 的比为多少时,储油灌的容积
的比为多少时,储油灌的容积 最大?
最大?
如图,已知直三棱柱 中,
中, ,
, ,
, ,D为BC的中点.
,D为BC的中点.
(1)求证: ∥面
∥面 ;
;
(2)求三棱锥 的体积.
的体积.
如图,在四棱锥 中,底面
中,底面 为直角梯形,且
为直角梯形,且 ,
, ,平面
,平面 底面
底面 ,
, 为
为 的中点,
的中点, 是棱
是棱 的中点,
的中点, .
.

(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求三棱锥 的体积.
的体积.
如图C,D是以AB为直径的圆上的两点, ,F是AB上的一点,且
,F是AB上的一点,且 ,将圆沿AB折起,使点C在平面ABD的射影E在BD上,已知
,将圆沿AB折起,使点C在平面ABD的射影E在BD上,已知


(1)求证:AD 平面BCE
平面BCE
(2)求证:AD//平面CEF;
(3)求三棱锥A-CFD的体积.
如图,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化了并流入杯中,会溢出杯子吗?请用你的计算数据说明理由。(冰、水的体积差异忽略不计)