[安徽]2013-2014学年安徽蚌埠高二第一学期期末考试理科数学试卷
抽查10件产品,设事件A:至少有两件次品,则A的对立事件为( )
| A.至多两件次品 | B.至多一件次品 |
| C.至多两件正品 | D.至少两件正品 |
已知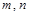 为两条不同直线,
为两条不同直线,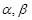 为两个不同平面,给出下列命题:
为两个不同平面,给出下列命题:
①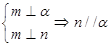 ②
②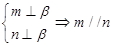
③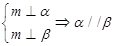 ④
④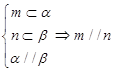
其中的正确命题序号( )
| A.③④ | B.②③ |
| C.①② | D.①②③④ |
如图,正三棱锥S—ABC中,∠BSC=40°,SB=2,一质点从点B出发,沿着三棱锥的侧面绕行一周回到点B的最短路线的长为( )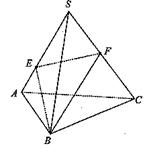
| A.2 | B.3 | C.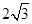 |
D.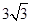 |
已知A(3,1),B(-1,2)若∠ACB的平分线方程为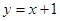 ,则AC所在的直线方程为( )
,则AC所在的直线方程为( )
A.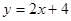 |
B.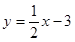 |
C.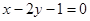 |
D.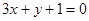 |
已知平面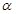 ∥平面
∥平面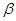 ,点P
,点P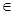 平面
平面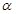 ,平面
,平面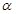 、
、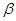 间的距离为8,则在
间的距离为8,则在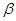 内到点P的距离为10的点的轨迹是( )
内到点P的距离为10的点的轨迹是( )
| A.一个圆 | B.四个点 |
| C.两条直线 | D.两个点 |
在正四棱锥P-ABCD中,PA=2,直线PA与平面ABCD所成角为60°,E为PC的中点,则异面直线PA与BE所成角为( )
A.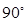 |
B.  |
C.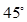 |
D.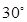 |
如果圆x2+y2-2ax-2ay+2a2-4=0与圆x2+y2=4总相交,则实数a的取值范围是_________.
利用如图算法在平面直角坐标系上打印一系列点,则打印的点既在直线2x-y+7=0右下方,又在直线x―2y+8=0左上方的有_____个.
给出以下结论:
①有两个侧面是矩形的棱柱是直棱柱;
②各侧面都是正方形的棱柱一定是正棱柱;
③对角面都是全等的矩形的直四棱柱一定是长方体;
④一个三棱锥四个面可以都为直角三角形;
⑤长方体一条对角线与同一个顶点的三条棱所成的角为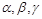 ,则
,则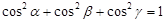 .
.
其中正确的是 .(将正确结论的序号全填上)
(1)求圆心在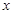 轴上,且与直线
轴上,且与直线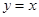 相切于点
相切于点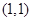 的圆的方程;
的圆的方程;
(2)已知圆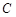 过点
过点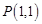 ,且与圆
,且与圆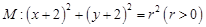 关于直线
关于直线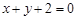 对称,求圆
对称,求圆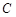 的方程.
的方程.
设x,y满足约束条件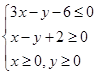 ,
,
(1)画出不等式表示的平面区域,并求该平面区域的面积;
(2)若目标函数z=ax+by(a>0,b>0)的最大值为4,求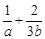 的最小值.
的最小值.
如图,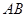 是圆柱体
是圆柱体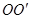 的一条母线,
的一条母线,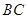 过底面圆的圆心
过底面圆的圆心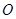 ,
,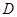 是圆
是圆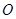 上不与点
上不与点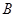 、
、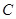 重合的任意一点,已知棱
重合的任意一点,已知棱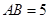 ,
,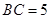 ,
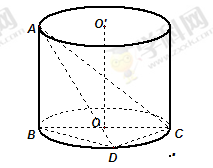
,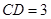 .
.
(1)求证: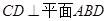 ;
;
(2)将四面体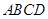 绕母线
绕母线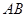 转动一周,求
转动一周,求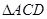 的三边在旋转过程中所围成的几何体的体积.
的三边在旋转过程中所围成的几何体的体积.
已知圆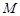 的方程为
的方程为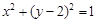 ,直线
,直线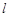 的方程为
的方程为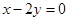 ,点
,点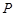 在直线
在直线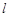 上,过
上,过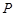 点作圆
点作圆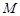 的切线
的切线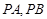 ,切点为
,切点为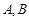 .
.
(1)若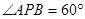 ,试求点
,试求点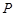 的坐标;
的坐标;
(2)若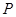 点的坐标为
点的坐标为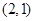 ,过
,过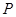 作直线与圆
作直线与圆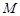 交于
交于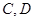 两点,当
两点,当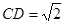 时,求直线
时,求直线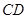 的方程;
的方程;
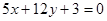 与
与 的距离是( )
的距离是( )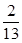
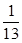
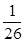
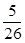
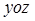 内的射影,则OB等于( )
内的射影,则OB等于( )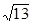
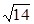
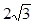
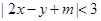 表示的平面区域包含点
表示的平面区域包含点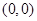 和
和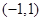 ,则实数
,则实数 的取值范围是( )
的取值范围是( )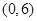
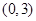
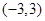
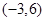
 -
-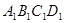 为正方体,下列结论错误的是( )
为正方体,下列结论错误的是( )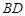 ∥
∥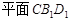
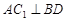
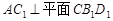
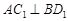
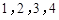 共4个数字中,任取两个数字(允许重复),其中一个数字是另一个数字的2倍的概率是 .
共4个数字中,任取两个数字(允许重复),其中一个数字是另一个数字的2倍的概率是 .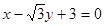 的倾斜角的大小是 .
的倾斜角的大小是 .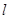 :
: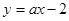 和
和 :
: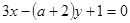 互相平行,求实数
互相平行,求实数 的值.
的值.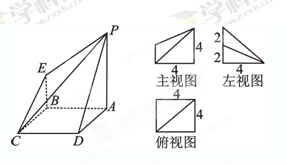
 为
为 的中点,求证:
的中点,求证: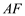
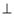 面
面 ;
; 面
面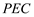 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号