如图,正三棱柱ABC-A'B'C'中,D是BC的中点,AA'=AB=2
(1)求证:AD B'D;
B'D;
(2)求三棱锥A'-AB'D的体积。
如图,在三棱锥 中,
中, ,
, ,D为AC的中点,
,D为AC的中点, .
.
(1)求证:平面 平面
平面 ;
;
(2)如果三棱锥 的体积为3,求
的体积为3,求 .
.
如图,四棱锥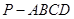 中,底面
中,底面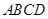 是边长为1的正方形,
是边长为1的正方形,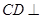 平面
平面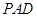 ,
, 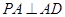 ,
,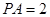 ,
,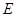 为
为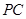 的中点,
的中点,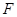 在棱
在棱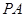 上.
上.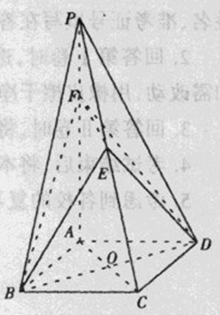
(1)求证: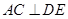 ;
;
(2)求三棱锥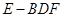 的体积.
的体积.
如图,正三棱锥 的底面边长为
的底面边长为 ,侧棱长为
,侧棱长为 ,
, 为棱
为棱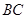 的中点.
的中点.
(1)求异面直线 与
与 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);
(2)求该三棱锥的体积 .
.
如图,正三棱锥 的底面边长为
的底面边长为 ,侧棱长为
,侧棱长为 ,
,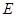 为棱
为棱 的中点.
的中点.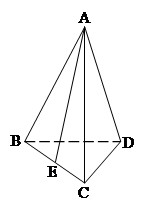
(1)求异面直线 与
与 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);
(2)求该三棱锥的体积 .
.
如图,正三棱柱ABC—A1B1C1的各棱长都相等,M、E分别是 和AB1的中点,点F在BC上且满足BF∶FC=1∶3.
和AB1的中点,点F在BC上且满足BF∶FC=1∶3.
(1)求证:BB1∥平面EFM;
(2)求四面体 的体积.
的体积.
如图,正三棱柱ABC—A1B1C1的各棱长都相等,M、E分别是 和AB1的中点,点F在BC上且满足BF∶FC=1∶3.
和AB1的中点,点F在BC上且满足BF∶FC=1∶3.
(1)求证:BB1∥平面EFM;
(2)求四面体 的体积.
的体积.
如图,在底面是正方形的四棱锥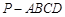 中,
中,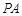
 面
面 ,
,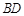 交
交 于点
于点 ,
,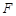 是
是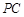 中点,
中点, 为
为 上一动点.
上一动点.
(1)求证: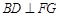 ;
;
(1)确定点 在线段
在线段 上的位置,使
上的位置,使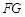 //平面
//平面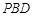 ,并说明理由.
,并说明理由.
(3)如果PA=AB=2,求三棱锥B-CDF的体积
(本小题满分12分)如图所示,矩形 的对角线交于点G,AD⊥平面
的对角线交于点G,AD⊥平面 ,
, ,
, ,
, 为
为 上的点,且BF⊥平面ACE
上的点,且BF⊥平面ACE
(1)求证: 平面
平面 ;
;
(2)求三棱锥 的体积.
的体积.
(本小题满分12分)在三棱柱 中,侧面
中,侧面 为矩形,
为矩形, ,
, ,
, 为
为 的中点,
的中点, 与
与 交于点
交于点 ,
, 侧面
侧面 .
.
(1)证明: ;
;
(2)若 ,求三棱锥
,求三棱锥 的体积.
的体积.
已知半径为 的球内有一个内接正方体(即正方体的顶点都在球面上).
的球内有一个内接正方体(即正方体的顶点都在球面上).
(1)求此球的体积;
(2)求此球的内接正方体的体积;
(3)求此球的表面积与其内接正方体的全面积之比.
已知正方体 的棱长为
的棱长为 .
.
(1)求异面直线 与
与 所成角的大小;
所成角的大小;
(2)求四棱锥 的体积.
的体积.
已知正方体 的棱长为
的棱长为 .
.
(1)求异面直线 与
与 所成角的大小;
所成角的大小;
(2)求四棱锥 的体积.
的体积.