[北京]2013-2014学年北京市西城区高二第一学期期末文科数学试卷
关于直线 以及平面
以及平面 ,下列命题中正确的是 ( )
,下列命题中正确的是 ( )
A.若 ,则 ,则 |
B.若 ,则 ,则 |
C.若 ,则 ,则 |
D.若 ,则 ,则 |
来源:2013-2014学年北京市西城区高二第一学期期末文科数学试卷
“ ”是“方程
”是“方程 表示圆”的 ( )
表示圆”的 ( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
来源:2013-2014学年北京市西城区高二第一学期期末文科数学试卷
若 ,则方程
,则方程 表示( )
表示( )
A.焦点在 轴上的椭圆 轴上的椭圆 |
B.焦点在 轴上的椭圆 轴上的椭圆 |
C.焦点在 轴上的双曲线 轴上的双曲线 |
D.焦点在 轴上的双曲线 轴上的双曲线 |
来源:2013-2014学年北京市西城区高二第一学期期末文科数学试卷
已知椭圆 ,
, 为坐标原点.若
为坐标原点.若 为椭圆上一点,且在
为椭圆上一点,且在 轴右侧,
轴右侧, 为
为 轴上一点,
轴上一点, ,则点
,则点 横坐标的最小值为( )
横坐标的最小值为( )
A. |
B. |
C. |
D. |
来源:2013-2014学年北京市西城区高二第一学期期末文科数学试卷
已知一个正方体的八个顶点都在同一个球面上,若此正方体的棱长为 ,那么这个球的表面积为_______.
,那么这个球的表面积为_______.
来源:2013-2014学年北京市西城区高二第一学期期末文科数学试卷
已知正方体 ,点
,点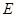 、
、 、
、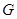 分别是棱
分别是棱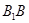 、
、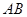 和
和 上的动点,观察直线
上的动点,观察直线 与
与 ,
, 与
与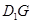 .
.
给出下列结论:
①对于任意点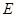 ,存在点
,存在点 ,使得
,使得
 ;②对于任意点
;②对于任意点 ,存在点
,存在点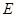 ,使得
,使得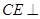
 ;
;
③对于任意点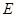 ,存在点
,存在点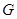 ,使得
,使得
 ;④对于任意点
;④对于任意点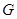 ,存在点
,存在点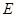 ,使得
,使得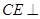
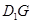 .
.
其中,所有正确结论的序号是__________.
来源:2013-2014学年北京市西城区高二第一学期期末文科数学试卷
已知圆 经过坐标原点
经过坐标原点 和点
和点 ,且圆心在
,且圆心在 轴上.
轴上.
(1)求圆 的方程;
的方程;
(2)设直线 经过点
经过点 ,且
,且 与圆
与圆 相交所得弦长为
相交所得弦长为 ,求直线
,求直线 的方程.
的方程.
来源:2013-2014学年北京市西城区高二第一学期期末文科数学试卷
在斜三棱柱 中,侧面
中,侧面 平面
平面 ,
, ,
, 为
为 中点.
中点.
(1)求证: ;
;
(2)求证: 平面
平面 ;
;
(3)若 ,
, ,求三棱锥
,求三棱锥 的体积.
的体积.
来源:2013-2014学年北京市西城区高二第一学期期末文科数学试卷
已知椭圆 的离心率为
的离心率为 ,左右焦点分别为
,左右焦点分别为 ,且
,且 .
.
(1)求椭圆C的方程;
(2)过点 的直线与椭圆
的直线与椭圆 相交于
相交于 两点,且
两点,且 ,求
,求 的面积.
的面积.
来源:2013-2014学年北京市西城区高二第一学期期末文科数学试卷
如图,四棱锥 中,底面
中,底面 为梯形,
为梯形, ,
, ,
, ,平面
,平面 平面
平面 ,
, .
.
(1)求证: 平面
平面 ;
;
(2)求证: ;
;
(3)是否存在点 ,到四棱锥
,到四棱锥 各顶点的距离都相等?并说明理由.
各顶点的距离都相等?并说明理由.
来源:2013-2014学年北京市西城区高二第一学期期末文科数学试卷
 的半径为 ( )
的半径为 ( )



 的实轴长为 ( )
的实轴长为 ( )



 为椭圆
为椭圆 上一点,
上一点,  为椭圆的两个焦点,且
为椭圆的两个焦点,且 , 则
, 则 ( )
( )



 ,
, ”的否定为( )
”的否定为( ) ,
,
 ,
, 
 中,下列结论不正确的是 ( )
中,下列结论不正确的是 ( )









 ,则其标准方程为_______.
,则其标准方程为_______. ,则
,则 ”的否命题是:__________________.
”的否命题是:__________________. 与圆
与圆 外切,则
外切,则 的值为_______.
的值为_______. 的离心率等于_______;渐近线方程为_______.
的离心率等于_______;渐近线方程为_______. 中,底面
中,底面 为矩形,
为矩形, 平面
平面 ,
, 为
为 中点.
中点.
 //平面
//平面 ;
; 平面
平面 ,点
,点 ,过
,过 的直线
的直线 交抛物线
交抛物线 于
于 两点.
两点. ,抛物线
,抛物线 中点的连线垂直于
中点的连线垂直于 轴,求直线
轴,求直线 为小于零的常数,点
为小于零的常数,点 关于
关于 ,求证:直线
,求证:直线 过定点
过定点 粤公网安备 44130202000953号
粤公网安备 44130202000953号