[江苏]2013-2014学年江苏省仪征市高二第一学期期末考试数学试卷

命题“”的否定是         ．

抛物线x＝8y²的焦点坐标为         ．

已知直线l⊥平面α，直线m⊂平面β，给出下列命题：
①若α∥β，则l⊥m；②若α⊥β，则l∥m；③若l∥m，则α⊥β；
④若l⊥m，则α∥β.其中正确命题的序号是________．

棱长为1的正方体的八个顶点都在同一个球面上，则此球的表面积为        ．

执行右边的程序框图6，若p＝0.8，则输出的n＝     ．

一组数据9.8， 9.9， 10，a， 10.2的平均数为10，则该组数据的方差为         .

曲线y=2lnx在点(e,2)处的切线与y轴交点的坐标为_________.

在区间上随机取一个数x，的值介于0到之间的概率为_____．

函数的单调减区间为___________.

某棉纺厂为了了解一批棉花的质量，从中随机抽取了100根棉花纤维的长度（棉花纤维的长度是棉花质量的重要指标），所得数据都在区间[5,40]中，其频率分布直方图如图所示，则其抽样的100根中，有________根的棉花纤维的长度小于20mm。

若函数f(x)＝e^x－2x－a在R上有两个零点，则实数a的取值范围是________．

已知函数()在区间上取得最小值4,则_      __.

已知是椭圆的一个焦点，是短轴的一个端点，线段的延长线交于点，且，则椭圆的离心率为____________．

已知函数y＝f(x)在定义域上可导，其图象如图，记y＝f(x)的导函数y＝f′(x)，则不等式xf′(x)≤0的解集是_______．

设命题p：函数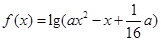的定义域为R；命题q：不等式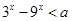对一切实数均成立。
（1）如果p是真命题，求实数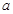的取值范围；
（2）如果命题“p或q”为真命题，且“p且q”为假命题，求实数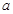的取值范围。

为了让学生了解更多“奥运会”知识，某中学举行了一次“奥运知识竞赛”，共有800名学生参加了这次竞赛. 为了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分均为整数，满分为100分）进行统计．请你根据尚未完成并有局部污损的频率分布表，解答下列问题：

 
(1)若用系统抽样的方法抽取50个样本，现将所有学生随机地编号为000，001，002，…799， 试写出第二组第一位学生的编号；
(2)填充频率分布表的空格(将答案直接填在表格内) ，并作出频率分布直方图；
(3)若成绩在85.5~95.5分的学生为二等奖，问参赛学生中获得二等奖的约多少人？

如图，四边形ABCD为矩形，AD 平面ABE,AE=EB=BC=2,F为CE上的点.且BF 平面ACE.

（1）求证：平面ADE平面BCE；
（2）求四棱锥E-ABCD的体积；
（3）设M在线段AB上，且满足AM=2MB，试在线段CE上确定一点N，使得MN平面DAE.

请您设计一个帐篷，它下部的形状是高为1m正六棱柱，上部的形状是侧棱长为3m的正六棱锥（如图所示）。试问当帐篷的顶点O到底面中心O₁的距离为多少时，帐篷的体积最大？

某地政府为科技兴市，欲在如图所示的矩形ABCD的非农业用地中规划出一个高科技工业园区（如图中阴影部分），形状为直角梯形QPRE（线段EQ和RP为两个底边），已知其中AF是以A为顶点、AD为对称轴的抛物线段．试求该高科技工业园区的最大面积．