如图,四边形ABCD为矩形,AD 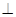 平面ABE,AE=EB=BC=2,F为CE上的点.且BF
平面ABE,AE=EB=BC=2,F为CE上的点.且BF 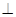 平面ACE.
平面ACE.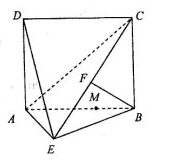
(1)求证:平面ADE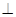 平面BCE;
平面BCE;
(2)求四棱锥E-ABCD的体积;
(3)设M在线段AB上,且满足AM=2MB,试在线段CE上确定一点N,使得MN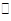 平面DAE.
平面DAE.
推荐套卷
如图,四边形ABCD为矩形,AD 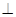 平面ABE,AE=EB=BC=2,F为CE上的点.且BF
平面ABE,AE=EB=BC=2,F为CE上的点.且BF 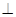 平面ACE.
平面ACE.
(1)求证:平面ADE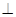 平面BCE;
平面BCE;
(2)求四棱锥E-ABCD的体积;
(3)设M在线段AB上,且满足AM=2MB,试在线段CE上确定一点N,使得MN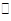 平面DAE.
平面DAE.