如图,已知正方形 的边长为
的边长为 ,点
,点 分别在边
分别在边 上,
上, ,现将△
,现将△ 沿线段
沿线段 折起到△
折起到△ 位置,使得
位置,使得 .
.
(1)求五棱锥 的体积;
的体积;
(2)在线段 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面 ?若存在,求
?若存在,求 ;若不存在,说明理由.
;若不存在,说明理由.
如图,已知正方形 的边长为
的边长为 ,点
,点 分别在边
分别在边 上,
上, ,现将△
,现将△ 沿线段
沿线段 折起到△
折起到△ 位置,使得
位置,使得 .
.
(1)求五棱锥 的体积;
的体积;
(2)求平面 与平面
与平面 的夹角.
的夹角.
如图,在体积为 的正三棱锥
的正三棱锥 中,
中,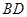 长为
长为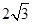 ,
, 为棱
为棱 的中点,求
的中点,求
(1)异面直线 与
与 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);
(2)正三棱锥 的表面积.
的表面积.
如图,在体积为 的正三棱锥
的正三棱锥 中,
中, 长为
长为 ,
, 为棱
为棱 的中点,求
的中点,求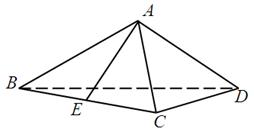
(1)异面直线 与
与 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);
(2)正三棱锥 的表面积.
的表面积.
如图所示,PA⊥平面ABCD,ABCD是矩形,AB=1, ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.
(1)若 ,求证:
,求证: ;
;
(2)若二面角 的大小为
的大小为 ,则CE为何值时,三棱锥
,则CE为何值时,三棱锥 的体积为
的体积为 .
.
如图所示的多面体中, 是菱形,
是菱形, 是矩形,
是矩形, 面
面 ,
, .
.
(1)求证:平 ;
;
(2)若 ,求四棱锥
,求四棱锥 的体积.
的体积.
如图,在△ABC中,∠ABC=90°,∠A=30。,斜边AC上的中线BD=2,现沿BD将△BCD折起成三棱锥C-ABD,已知G是线段BD的中点,E,F分别是CG,AG的中点.
(1)求证:EF//平面ABC;
(2)三棱锥C—ABD中,若棱AC= ,求三棱锥A一BCD的体积.
,求三棱锥A一BCD的体积.
如图1,在直角梯形 中,
中, ,
, .把
.把 沿
沿 折起到
折起到 的位置,使得
的位置,使得 点在平面
点在平面 上的正投影
上的正投影 恰好落在线段
恰好落在线段 上,如图2所示,点
上,如图2所示,点 分别为棱
分别为棱 的中点.
的中点.
(1)求证:平面 平面
平面 ;
;
(2)求证: 平面
平面 ;
;
(3)若 ,求四棱锥
,求四棱锥 的体积.
的体积.
如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点, 是AC的中点,已知
是AC的中点,已知 ,
, .
.
(1)求证:OD//平面VBC;
(2)求证:AC⊥平面VOD;
(3)求棱锥 的体积.
的体积.
如图, 已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且 ,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
(1)求证: EC⊥CD ;
(2)求证:AG∥平面BDE;
(3)求:几何体EG-ABCD的体积.
如图,△ 中,
中, ,
, ,
, ,在三角形内挖去一个半圆(圆心
,在三角形内挖去一个半圆(圆心 在边
在边 上,半圆与
上,半圆与 、
、 分别相切于点
分别相切于点 、
、 ,与
,与 交于点
交于点 ),将△
),将△ 绕直线
绕直线 旋转一周得到一个旋转体.
旋转一周得到一个旋转体.
(1)求该几何体中间一个空心球的表面积的大小;
(2)求图中阴影部分绕直线 旋转一周所得旋转体的体积.
旋转一周所得旋转体的体积.
如图,在四棱锥P - ABCD中,平面PAD⊥平面ABCD,AB∥DC,
△PAD是等边三角形,已知BD ="2AD" =8,AB ="2DC" = .
.

(I)设M是PC上的一点,证明:平面MBD 平面PAD;
平面PAD;
(Ⅱ)求三棱锥C—PAB的体积.
(本小题满分12分)
如图,在三棱锥 中,⊿
中,⊿ 是等边三角形,
是等边三角形, 是以
是以 为斜边的等腰直角三角形.
为斜边的等腰直角三角形.
(Ⅰ)证明:AB⊥PC;
(Ⅱ) ,求三棱锥
,求三棱锥 体积.
体积.
菱形 的边长为3,
的边长为3, 与
与 交于
交于 ,且
,且 .将菱形
.将菱形 沿对角线
沿对角线 折起得到三棱锥
折起得到三棱锥 (如图),点
(如图),点 是棱
是棱 的中点,
的中点, .
.
(1)求证:平面
 平面
平面 ;
;
(2)求三棱锥 的体积.
的体积.