已知四边形 满足
满足 ,
, ,
, 是
是 的中点,将
的中点,将 沿着
沿着 翻折成
翻折成 ,使面
,使面 面
面 ,
, 分别为
分别为
 的中点.
的中点. 

(1)求三棱锥 的体积;
的体积;
(2)证明: ∥平面
∥平面 ;
;
(3)证明:平面 平面
平面
某几何体的三视图如图所示,其中俯视图为半径为 的四分之一个圆弧,则该几何体的体积为.
的四分之一个圆弧,则该几何体的体积为.
如图所示是一个几何体的三视图,则这个几何体外接球的表面积为()
A.8 |
B.16 |
C.32 |
D.64 |
如图是一个几何体的三视图,则该几何体的体积是()
| A.54 | B.27 | C.18 | D.9 |
某几何体的三视图如图所示,则该几何体的体积为 ()
A. |
B. |
C. |
D. |
一个几何体的三视图如图所示,则该几何体的体积的是() 
A. |
B. |
C. |
D. |
一个四棱锥的三视图如图所示,其中侧视图为正三角形,则该四棱锥的体积是,四棱锥侧面中最大侧面的面积是.
如图,网格纸上小正方形边长为1,粗线是一个棱锥的三视图,则此棱锥的表面积为()
A. |
B. |
C. |
D. |
(本小题满分14分)四棱锥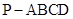 中,
中,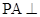 底面
底面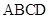 ,
,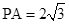 ,
,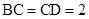 ,
,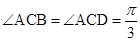 .
.
(1)求证: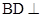 平面
平面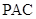 ;
;
(2)若侧棱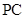 上的点
上的点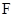 满足
满足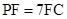 ,求三棱锥
,求三棱锥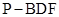 的体积.
的体积.