北京市朝阳区高三第一次综合练习文科数学试卷
已知边长为3的正方形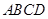 与正方形
与正方形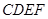 所在的平面互相垂直,
所在的平面互相垂直,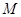 为线段
为线段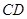 上的动点(不含端点),过
上的动点(不含端点),过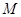 作
作 交
交 于
于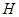 ,作
,作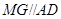 交
交 于
于 ,连结
,连结 .设
.设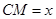
 ,则下面四个图象中大致描绘了三棱锥
,则下面四个图象中大致描绘了三棱锥 的体积
的体积 与变量
与变量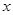 变化关系的是
变化关系的是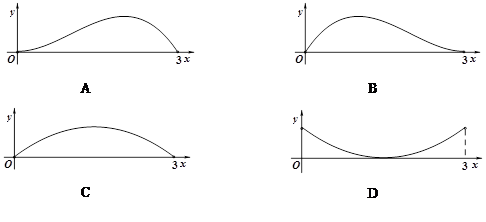
一个四棱锥的三视图如图所示,其中侧视图为正三角形,则该四棱锥的体积是 ,四棱锥侧面中最大侧面的面积是 .
稿酬所得以个人每次取得的收入,定额或定率减除规定费用后的余额为应纳税所得额,每次收入不超过4000元,定额减除费用800元;每次收入在4000元以上的,定率减除20%的费用.适用20%的比例税率,并按规定对应纳税额减征30%,计算公式为:
(1)每次收入不超过4000元的:应纳税额=(每次收入额-800)×20%×(1-30%)
(2)每次收入在4000元以上的:应纳税额=每次收入额×(1-20%)×20%×(1-30%).已知某人出版一份书稿,共纳税280元,这个人应得稿费(扣税前)为 元.
(本小题满分13分)某次考试结束后,为了解甲、乙两所学校学生的数学考试情况,随机抽取甲、乙两校各10名学生的考试成绩,得茎叶图如图所示(部分数据不清晰):
(Ⅰ)请根据茎叶图判断哪个学校的数学成绩平均水平较高(直接写出结果);
(Ⅱ)若在抽到的这20名学生中,分别从甲、乙两校随机各抽取1名成绩不低于90分的学生,求抽到的学生中, 甲校学生成绩高于乙校学生成绩的概率.
(本小题满分14分)如图,在三棱柱 中,各个侧面均是边长为
中,各个侧面均是边长为 的正方形,
的正方形, 为线段
为线段 的中点.
的中点.
(Ⅰ)求证: ⊥平面
⊥平面 ;
;
(Ⅱ)求证:直线 ∥平面
∥平面 ;
;
(Ⅲ)设 为线段
为线段 上任意一点,在
上任意一点,在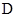
 内的平面区域(包括边界)是否存在点
内的平面区域(包括边界)是否存在点 ,使
,使
 ,并说明理由.
,并说明理由.
(本小题满分13分)设数列 的前
的前 项和为
项和为 ,且
,且 ,
, ,
, .
.
(Ⅰ)写出 ,
, ,
, 的值;
的值;
(Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)已知等差数列 中,有
中,有 ,
,  ,求数列
,求数列 的前
的前 项和
项和 .
.
(本小题满分14分)已知椭圆 的两个焦点分别为
的两个焦点分别为 ,离心率为
,离心率为 .过焦点
.过焦点 的直线
的直线 (斜率不为0)与椭圆
(斜率不为0)与椭圆 交于
交于 两点,线段
两点,线段 的中点为
的中点为 ,
, 为坐标原点,直线
为坐标原点,直线 交椭圆于
交椭圆于 两点.
两点.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)当四边形 为矩形时,求直线
为矩形时,求直线 的方程.
的方程.
 ,集合
,集合 ,则
,则 等于
等于




 ,
, ,则
,则


 ,
, 

 的焦点与双曲线
的焦点与双曲线 的右焦点重合,则
的右焦点重合,则 的值为
的值为




 的值
的值 的值
的值 的值
的值 的值
的值 ,
, ,
, 满足
满足 ,则
,则



 图象的一条对称轴方程是
图象的一条对称轴方程是



 ,
, 满足
满足 其中
其中 .若
.若 的最大值为5,则z的最小值为
的最大值为5,则z的最小值为



 为虚数单位,计算
为虚数单位,计算 = .
= . ,
, 满足
满足 ,
, ,则
,则 .
. 与
与 轴相交于
轴相交于 两点,则弦
两点,则弦 所对的圆心角的大小为 .
所对的圆心角的大小为 . 为区间
为区间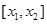 的长度.已知函数
的长度.已知函数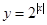 ,
,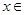
 (
(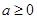 ),其值域为
),其值域为 ,则区间
,则区间 中,
中, ,
, ,
, .
. 的长;
的长; ,
, .
. 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程; 时,求证:
时,求证: 在
在 上为增函数;
上为增函数; 上有且只有一个极值点,求
上有且只有一个极值点,求 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号