已知函数f(x)在区间(-∞,+∞)上是增函数,a,b∈R.
(1)求证:若a+b≥0,则f(a)+f(b)≥f(-a)+f(-b);
(2)判断(1)中命题的逆命题是否正确,并证明你的结论.
已知c>0,设命题p:函数y=cx为减函数.命题q:当x∈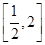 时,函数f(x)=x+
时,函数f(x)=x+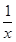 >
> 恒成立.如果p或q为真命题,p且q为假命题,求c的取值范围.
恒成立.如果p或q为真命题,p且q为假命题,求c的取值范围.
已知集合A={x|x2-4mx+2m+6=0},B={x|x<0},若命题“A∩B=∅”是假命题,求实数m的取值范围.
设 :
: ,
, :关于
:关于 的不等式
的不等式 的解集是空集,试确定实数
的解集是空集,试确定实数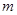 的取值范围,使得
的取值范围,使得 或
或 为真命题,
为真命题, 且
且 为假命题.
为假命题.
已知 ,设p:函数
,设p:函数 在(0,+∞)上单调递减,
在(0,+∞)上单调递减,
q:曲线y=x2+(2a 3)x+1与x轴交于不同的两点.若“p且q”为假,“﹁q”为假,求a的取值范围.
已知a∈R,设p:函数f(x)=x2+(a-1)x是区间(1,+∞)上的增函数,q:方程x2-ay2=1表示双曲线.
(1)若p为真命题,求实数a的取值范围;
(2)若“p且q”为真命题,求实数a的取值范围.
设命题p:关于x的不等式2|x-2|<a的解集为;命题q:函数y=lg(ax2-x+a)的值域是R.如果命题p和q有且仅有一个正确,求实数a的取值范围.
已知命题p:函数y=loga(1-2x)在定义域上单调递增;命题q:不等式(a-2)x2+2(a-2)x-4<0对任意实数x恒成立.若p∨q是真命题,求实数a的取值范围.
已知命题p:方程a2x2+ax-2=0在[-1,1]上有解;命题q:只有一个实数x满足不等式x2+2ax+2a≤0,若命题“p或q”是假命题,求实数a的取值范围.