命题“存在一个无理数,它的平方是有理数”的否定是( )
| A.任意一个有理数,它的平方是有理数 |
| B.任意一个无理数,它的平方不是有理数 |
| C.存在一个有理数,它的平方是有理数 |
| D.存在一个无理数,它的平方不是有理数 |
命题“若a2+b2=0,则a=0且b=0”的逆否命题是( )
| A.若a2+b2≠0,则a≠0且b≠0 | B.若a2+b2≠0,则a≠0或b≠0 |
| C.若a=0且b=0,则a2+b2≠0 | D.若a≠0或b≠0,则a2+b2≠0 |
有下列四个命题:
①“若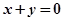 , 则
, 则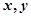 互为相反数”的逆命题;
互为相反数”的逆命题;
②“全等三角形的面积相等”的否命题;
③“若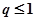 ,则
,则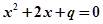 有实根”的逆否命题;
有实根”的逆否命题;
④“存在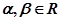 ,使
,使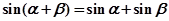 成立”的否定.
成立”的否定.
其中真命题为( )
| A.①② | B.②③ | C.①③ | D.③④ |
给出下列说法:
①命题“若α= ,则sinα=
,则sinα= ”的否命题是假命题;
”的否命题是假命题;
②命题p:∃x∈R,使sinx>1,则 p:∀x∈R,sinx≤1;
p:∀x∈R,sinx≤1;
③“φ= +2kπ(k∈Z)”是“函数y=sin(2x+φ)为偶函数”的充要条件;
+2kπ(k∈Z)”是“函数y=sin(2x+φ)为偶函数”的充要条件;
④命题p:∃x∈(0, ),使sinx+cosx=
),使sinx+cosx= ,命题q:在△ABC中,若sinA>sinB,则A>B,那么命题(
,命题q:在△ABC中,若sinA>sinB,则A>B,那么命题( p)∧q为真命题.
p)∧q为真命题.
其中正确的个数是( )
| A.4 | B.3 | C.2 | D.1 |
已知命题P:关于x的方程x2-ax+4=0有实根;命题Q:关于x的函数y=2x2+ax+4在[3,+∞)上是增函数.若P或Q是真命题,P且Q是假命题,则实数a的取值范围是( )
| A.(-12,-4]∪[4,+∞) |
| B.[-12,-4]∪[4,+∞) |
| C.(-∞,-12)∪(-4,4) |
| D.[-12,+∞) |
已知命题p:若x>0,y>0,则xy>0,则p的否命题是( )
| A.若x>0,y>0,则xy≤0 |
| B.若x≤0,y≤0,则xy≤0 |
| C.若x,y至少有一个不大于0,则xy<0 |
| D.若x,y至少有一个小于或等于0,则xy≤0 |
下列命题中的假命题是( )
A. |
B.“ ”是“ ”是“ ”的充分不必要条件 ”的充分不必要条件 |
C. |
D.若 为假命题,则 为假命题,则 、 、 均为假命题 均为假命题 |
下列命题是真命题的是( )
| A.单位向量都相等 |
| B.若a与b共线,b与c共线,则a与c共线 |
| C.若|a+b|=|a-b|,则a·b=0 |
| D.若a与b都是单位向量,则a·b=1 |
下列命题中正确命题的个数是( )
(1)命题“若 ,则
,则 ”的逆否命题为“若
”的逆否命题为“若 ,则
,则 ”;
”;
(2)设回归直线方程 中,
中, 增加1个单位时,
增加1个单位时, 一定增加2个单位;
一定增加2个单位;
(3)若 为假命题,则
为假命题,则 均为假命题;
均为假命题;
(4)对命题 ,使得
,使得 ,则
,则 ,均有
,均有 ;
;
(5)设随机变量 服从正态分布
服从正态分布 ,若
,若 ,则
,则 .
.
| A.2 | B.3 | C.4 | D.5 |
命题“对任意的 ,都有
,都有 ”的否定为
”的否定为
A.存在 ,使 ,使 |
B.对任意的 ,都有 ,都有 |
C.存在 ,使 ,使 |
D.存在 ,使 ,使 |
设命题p:函数y=sin2x的最小正周期为 ;命题q:函数y=cosx的图象关于直线
;命题q:函数y=cosx的图象关于直线 对称.则下列判断正确的是( )
对称.则下列判断正确的是( )
| A.p为真 | B.¬q为假 | C.p q为真 q为真 |
D.p q为假 q为假 |
命题“若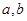 都是奇数,则
都是奇数,则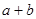 是偶数”的逆否命题是( )
是偶数”的逆否命题是( )
A.若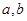 都不是奇数,则 都不是奇数,则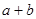 是偶数 是偶数 |
B.若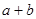 是偶数,则 是偶数,则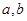 都是奇数 都是奇数 |
C.若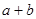 不是偶数,则 不是偶数,则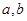 都不是奇数 都不是奇数 |
D.若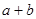 不是偶数,则 不是偶数,则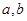 不都是奇数 不都是奇数 |
命题“若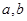 都是奇数,则
都是奇数,则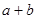 是偶数”的逆否命题是( )
是偶数”的逆否命题是( )
A.若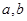 都不是奇数,则 都不是奇数,则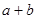 是偶数 是偶数 |
B.若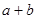 是偶数,则 是偶数,则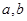 都是奇数 都是奇数 |
C.若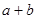 不是偶数,则 不是偶数,则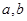 都不是奇数 都不是奇数 |
D.若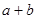 不是偶数,则 不是偶数,则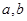 不都是奇数 不都是奇数 |