广东省“十二校”高三第2次联考文科数学试卷
下列命题中的假命题是( )
A. |
B.“ ”是“ ”是“ ”的充分不必要条件 ”的充分不必要条件 |
C. |
D.若 为假命题,则 为假命题,则 、 、 均为假命题 均为假命题 |
来源:2014届广东省“十二校”高三第2次联考文科数学试卷
若直线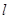 不平行于平面
不平行于平面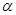 ,且
,且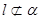 ,则( )
,则( )
A.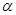 内的所有直线与 内的所有直线与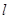 异面 异面 |
B.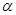 内存在唯一的直线与 内存在唯一的直线与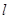 平行 平行 |
C.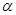 内不存在与 内不存在与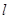 平行的直线 平行的直线 |
D.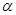 内的直线都与 内的直线都与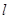 都相交 都相交 |
来源:2014届广东省“十二校”高三第2次联考文科数学试卷
 是
是 所在的平面内的一点,且满足
所在的平面内的一点,且满足 ,则
,则 的形状一定为( )
的形状一定为( )
| A.正三角形 | B.直角三角形 | C.等腰三角形 | D.斜三角形 |
来源:2014届广东省“十二校”高三第2次联考文科数学试卷
已知平面直角坐标系 上的区域
上的区域 由不等式组
由不等式组 给定,若
给定,若 为
为 上的动点,点
上的动点,点 ,则
,则 的最大值为 ( )
的最大值为 ( )
| A.6 | B. |
C.4 | D.2 |
来源:2014届广东省“十二校”高三第2次联考文科数学试卷
某单位有200名职工,现用系统抽样法,从中抽取40名职工作样本,将全体职工随机按1-200编号,并按编号顺序平均分为40组(1-5号,6-10号…,196-200号).若第5组抽出的号码为22,则第9组抽出的号码应是
来源:2014届广东省“十二校”高三第2次联考文科数学试卷
为了了解某年段1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);……;第五组[17,18].按上述分组方法得到的频率分布直方图如图3所示,已知图中从左到右的前3个组的频率之比为3∶8∶19,且第二组的频数为8.
(1)将频率当作概率,请估计该年段学生中百米成绩在[16,17)内的人数;
(2)求调查中随机抽取了多少个学生的百米成绩;
(3)若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值大于1秒的概率.
来源:2014届广东省“十二校”高三第2次联考文科数学试卷
一个几何体是由圆柱 和三棱锥
和三棱锥 组合而成,点
组合而成,点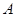 、
、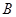 、
、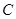 在圆
在圆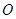 的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图4所示,其中
的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图4所示,其中 ,
, ,
,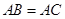 ,
, .
.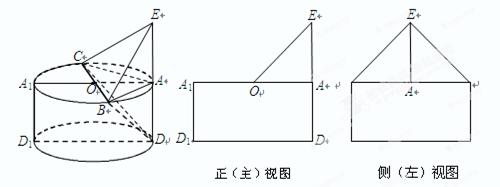
(1)求证: ;
;
(2)求三棱锥 的体积.
的体积.
来源:2014届广东省“十二校”高三第2次联考文科数学试卷
已知数列 (常数
(常数 ),其前
),其前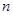 项和为
项和为
 (
( )
)
(1)求数列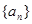 的首项
的首项 ,并判断
,并判断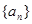 是否为等差数列,若是求其通项公式,不是,说明理由;
是否为等差数列,若是求其通项公式,不是,说明理由;
(2)令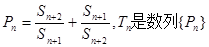 的前n项和,求证:
的前n项和,求证: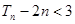
来源:2014届广东省“十二校”高三第2次联考文科数学试卷
如图,椭圆 的左焦点为
的左焦点为 ,右焦点为
,右焦点为 ,过
,过 的直线交椭圆于
的直线交椭圆于 两点,
两点, 的周长为8,且
的周长为8,且 面积最大时,
面积最大时, 为正三角形.
为正三角形.
(1)求椭圆 的方程;
的方程;
(2)设动直线 与椭圆
与椭圆 有且只有一个公共点
有且只有一个公共点 ,且与直线
,且与直线 相交于点
相交于点 ,证明:点
,证明:点 在以
在以 为直径的圆上.
为直径的圆上.
来源:2014届广东省“十二校”高三第2次联考文科数学试卷
 ,若
,若 (
( 为虚数单位)为正实数,则
为虚数单位)为正实数,则 ( )
( )
 ,则( )
,则( )



 中,
中, ,则
,则 的值是( )
的值是( )
 经过双曲线
经过双曲线 左焦点且与直线
左焦点且与直线 相切,则圆心
相切,则圆心



 是函数
是函数 的零点,若
的零点,若 ,则
,则 的值满足( )
的值满足( )


 中,
中, 、
、 、
、 分别是角A、B、C所对的边,
分别是角A、B、C所对的边, ,则
,则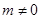 ,函数
,函数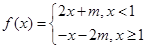 ,若
,若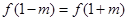 ,则
,则 的值为________.
的值为________.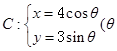 为参数,
为参数, 上一点,O为原点.若直线OP的倾斜角为
上一点,O为原点.若直线OP的倾斜角为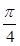 ,则点
,则点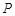 的直角坐标为 .
的直角坐标为 . 和
和 相交于
相交于 两点,过
两点,过 作两圆的切线分别交两圆于
作两圆的切线分别交两圆于 、
、 两点,连接
两点,连接 、
、 ,已知
,已知 ,
, ,则
,则 .
.
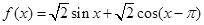 .
.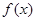 的最小正周期和值域;
的最小正周期和值域;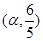 ,
,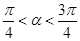 .求
.求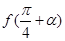 的值.
的值.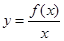 在
在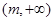 上为增函数(
上为增函数(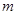 为常数),则称
为常数),则称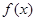 为区间
为区间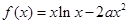 是
是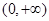 上的“一阶比增函数”,求实数
上的“一阶比增函数”,求实数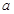 的取值范围;
的取值范围;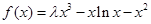 (
(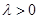 ,
,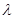 为常数),且
为常数),且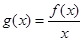 有唯一的零点,求
有唯一的零点,求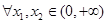 ,
,
 粤公网安备 44130202000953号
粤公网安备 44130202000953号