已知二次函数
(1)若 试判断函数
试判断函数 零点个数;
零点个数;
(2)若对任意的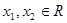 ,且
,且 <
<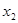 ,
,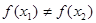 (
(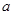 >0),试证明:
>0),试证明: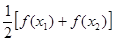 >
> 成立。
成立。
(3)是否存在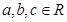 ,使
,使 同时满足以下条件:①对任意
同时满足以下条件:①对任意 ,
, ,且
,且 ②对任意的
②对任意的 ,都有
,都有 ?若存在,求出
?若存在,求出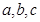 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
(本小题满分12分)美国华尔街的次贷危机引起的金融风暴席卷全球,低迷的市场造成产品销售越来越难,为此某厂家举行大型的促销活动,经测算该产品的销售量P万件(生产量与销售量相等)与促销费用 万元满足
万元满足 ,已知生产该产品还需投入成本
,已知生产该产品还需投入成本 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为 元/万件.
元/万件.
(Ⅰ)将该产品的利润 万元表示为促销费用
万元表示为促销费用 万元的函数;
万元的函数;
(Ⅱ)促销费用投入多少万元时,厂家的利润最大。
已知函数f(x)= -
- (a>0,x>0).
(a>0,x>0).
(1)用函数的单调性定义证明:f(x)在(0,+∞)上是增函数;
(2)若f(x)在[ ,2]上的值域是[
,2]上的值域是[ ,2],求实数a的值.
,2],求实数a的值.
(本小题满分14分)某城市自西向东和自南向北的两条主干道的东南方位有一块空地市规划部门计划利用它建设一个供市民休闲健身的小型绿化广场,如下图所示是步行小道设计方案示意图,
其中, 分别表示自西向东,自南向北的两条主干道.设计方案是自主干道交汇点
分别表示自西向东,自南向北的两条主干道.设计方案是自主干道交汇点 处修一条步行小道,小道为抛物线
处修一条步行小道,小道为抛物线 的一段,在小道上依次以点
的一段,在小道上依次以点 为圆心,修一系列圆型小道,这些圆型小道与主干道
为圆心,修一系列圆型小道,这些圆型小道与主干道 相切,且任意相邻的两圆彼此外切,若
相切,且任意相邻的两圆彼此外切,若 (单位:百米)且
(单位:百米)且 .
.
(1)记以 为圆心的圆与主干道
为圆心的圆与主干道 切于
切于 点,证明:数列
点,证明:数列 是等差数列,并求
是等差数列,并求 关于
关于 的表达式;
的表达式;
(2)记 的面积为
的面积为 ,根据以往施工经验可知,面积为
,根据以往施工经验可知,面积为 的圆型小道的施工工时为
的圆型小道的施工工时为 (单位:周).试问5周时间内能否完成前
(单位:周).试问5周时间内能否完成前 个圆型小道的修建?请说明你的理由.
个圆型小道的修建?请说明你的理由.