已知函数 ,点
,点 .
.
(Ⅰ)若 ,函数
,函数 在
在 上既能取到极大值,又能取到极小值,求
上既能取到极大值,又能取到极小值,求 的取值范围;
的取值范围;
(Ⅱ) 当 时,
时, 对任意的
对任意的 恒成立,求
恒成立,求 的取值范围;
的取值范围;
(Ⅲ)若 ,函数
,函数 在
在 和
和 处取得极值,且
处取得极值,且 ,
, 是坐标原点,证明:直线
是坐标原点,证明:直线 与直线
与直线 不可能垂直.
不可能垂直.
某产品的广告费用x与销售额y的统计数据如下表
根据上表可得回归方程 中的
中的 为9.4,据此模型预报广告费用为6万元时销售额为( )
为9.4,据此模型预报广告费用为6万元时销售额为( )
| A.63.6万元 | B.65.5万元 | C.67.7万元 | D.72.0万元 |
(本小题满分12分)养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用).已建仓库的底面直径为12m,高4m.养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大4m(高不变);二是高度增加4m(底面直径不变).
(1)分别计算按这两种方案所建的仓库的体积;
(2)分别计算按这两种方案所建的仓库的表面积(底面面积不计);
(3)哪个方案更经济些?
设
,已知函数
.
(Ⅰ)当
时,讨论函数
的单调性;
(Ⅱ)当
时,称
为
关于
的加权平均数.
(1)判断
是否成等比数列,并证明
;
(2)
的几何平均数记为
.称
为
的调和平均数,记为
.若
,求
的取值范围.
下列函数中,既是偶函数,又在区间(1,2)内是增函数的为( )
| A.y=cos 2x,x∈R |
| B.y=log2|x|,x∈R且x≠0 |
C.y=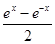 ,x∈R ,x∈R |
| D.y=x3+1,x∈R |