(本小题满分12分)如图,在平面直角坐标系 中,点
中,点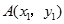 在单位圆
在单位圆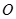 上,
上, ,且
,且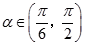 .
.
(1)若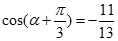 ,求
,求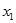 的值;
的值;
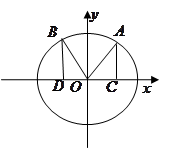
(2)若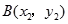 也是单位圆
也是单位圆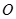 上的点,且
上的点,且 .过点
.过点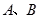 分别做
分别做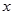 轴的垂线,垂足为
轴的垂线,垂足为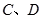 ,记
,记 的面积为
的面积为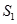 ,
,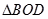 的面积为
的面积为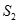 .设
.设 ,求函数
,求函数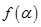 的最大值.
的最大值.
(本小题满分12分)
已知向量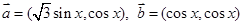 ,函数
,函数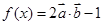
(1)求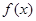 的单调递增区间;
的单调递增区间;
(2)当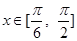 时, 若
时, 若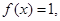 求
求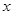 的值。
的值。
已知函数
(Ⅰ)求函数y = f(x)的单调递增区间;
(Ⅱ)当x ∈ [0, ] 时,函数 y = f(x)的最小值为
] 时,函数 y = f(x)的最小值为  ,试确定常数a的值.
,试确定常数a的值.
(本小题满分14分)函数 ,(
,( )的最小正周期为
)的最小正周期为 ,且在
,且在 处取得最小值
处取得最小值 .
.
(Ⅰ)求 的单调递增区间;
的单调递增区间;
(Ⅱ)将 的图象向左平移
的图象向左平移 个单位后得到函数
个单位后得到函数 ,设
,设 为三角形的三个内角,若
为三角形的三个内角,若 ,且
,且 ,求
,求 的取值范围.
的取值范围.
已知函数
在x=
时取得最大值4..
(1)求
的最小正周期;
(2)求
的解析式;
(3)若
.求
的值.