将函数 的图像上所有的点向右平行移动
的图像上所有的点向右平行移动 个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图像的函数解析式是
个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图像的函数解析式是

 ( )
( )
A. |
B. |
C. |
D. |
. (12分)如图所示,函数 的一段图象过点
的一段图象过点 .
.
(1)求函数 的表达式;
的表达式;
(2)将函数 的图象向右平移
的图象向右平移 个单位,得函数
个单位,得函数 的图象,求函数
的图象,求函数 的最大值,并求此时自变量
的最大值,并求此时自变量 的取值集合.
的取值集合.
(本小题满分12分)
已知函数 .
.
(Ⅰ)求函数 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(Ⅱ)函数 的图象可由函数
的图象可由函数 的图象经过怎样的变换得出?
的图象经过怎样的变换得出?
如图所示,某市政府决定在以政府大楼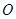 为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径
为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径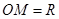 ,
,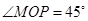 ,
, 与
与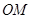 之间的夹角为
之间的夹角为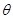 .
.
(1)将图书馆底面矩形 的面积
的面积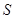 表示成
表示成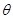 的函数.
的函数.
(2)若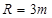 ,求当
,求当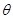 为何值时,矩形
为何值时,矩形 的面积
的面积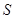 有最大值?
有最大值?
其最大值是多少?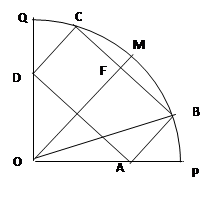
设函数 ,其中向量
,其中向量 ,
,
(1)求 的最小正周期与单调减区间;
的最小正周期与单调减区间;
(2)在△ABC中, 分别是角A、B、C的对边,已知
分别是角A、B、C的对边,已知 ,△ABC的面积为
,△ABC的面积为 ,求
,求 的值。
的值。
设函数 ,其中向量
,其中向量 =(2cosx,1),
=(2cosx,1), =(cosx,
=(cosx, sin2x),x∈R.
sin2x),x∈R.
(1)若f(x)=1- 且x∈[-
且x∈[- ,
, ],求x;
],求x;
(2)若函数y=2sin2x的图象按向量 =(m,n)(|m|<
=(m,n)(|m|< )平移后得到函数y=f(x)的图象,求实数m、n的值.
)平移后得到函数y=f(x)的图象,求实数m、n的值.
(本小题满分13分)已知函数 ,
, .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的最大值和最小值.
的最大值和最小值.
(本小题满分13分)已知函数 ,
, .
.
(Ⅰ)求 的零点;
的零点;
(Ⅱ)求 的最大值和最小值.
的最大值和最小值.
(本题14分,第(1)小题4分,第(2)小题10分).
已知:函数 .
.
(1)求 的值;
的值;
(2)设 ,
, ,求
,求 的值.
的值.
已知函数
 ,下面结论错误的是 ………( )
,下面结论错误的是 ………( )
A.函数 的最小正周期为 的最小正周期为 |
B.函数 是奇函数 是奇函数 |
C.函数 在 在 时,取得最小值 时,取得最小值 |
D.函数 在区间 在区间 上是减函数 上是减函数 |