设函数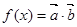
，其中向量
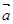=(2cosx，1)，
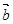=(cosx，
sin2x)，x∈R.
（1）若f(x)=1－且x∈[－
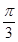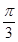，]，求x；
（2）若函数y=2sin2x的图象按向量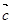
=(m，n)(|m|<
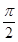)平移后得到函数y=f(x)的图象，求实数m、n的值．
数列
满足：
是等比数列（要指出首项与公比）, 
的通项公式.
与
互相垂直，其中
．
和
的值；（2）若
，求
的值.
、
、
为
的三内角，且其对边分别为
、
、
，若
．
，求
,
,
,
,求
的取值范围。相关知识点
推荐套卷
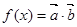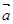设函数，其中向量=(2cosx，1)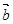，=(cosx，sin2x)，x∈R.
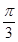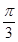（1）若f(x)=1－且x∈[－，]，求x；
（2）若函数y=2sin2x的图象按向量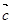=(m，n)(|m|<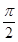)平移后得到函数y=f(x)的图象，求实数m、n的值．
粤公网安备 44130202000953号