已知 ,命题
,命题 ,命题
,命题 .
.
(I)若命题 为真命题,求实数
为真命题,求实数 的取值范围;
的取值范围;
(II)若命题 为假命题,求实数
为假命题,求实数 的取值范围.
的取值范围.
命题 实数x满足
实数x满足 (其中
(其中 ),命题
),命题

(Ⅰ)若 ,且
,且 为真,求实数
为真,求实数 的取值范围;
的取值范围;
(Ⅱ)若q是p的充分不必要条件,求实数a的取值范围.
已知命题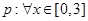 ,
,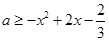 ,命题
,命题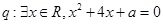 ,若命题“
,若命题“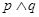 ”是真命题,求实数a的取值范围.
”是真命题,求实数a的取值范围.
已知命题 ,命题
,命题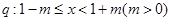 。
。
(1)若p是q的充分条件,求实数m的取值范围;
(2)若m=5,“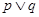 ”为真命题,“
”为真命题,“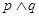 ”为假命题,求实数x的取值范围。
”为假命题,求实数x的取值范围。
(本小题满分12分)命题 :关于x的不等式x2+2ax+4>0对一切x∈R恒成立,
:关于x的不等式x2+2ax+4>0对一切x∈R恒成立, :函数f(x)=(3-2a)x是增函数.若
:函数f(x)=(3-2a)x是增函数.若 为真,
为真, 为假.求实数a的取值范围.
为假.求实数a的取值范围.
下列命题错误的是( )
A.命题“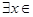 R使得 R使得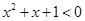 ”的否定是:“ ”的否定是:“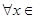 R均有 R均有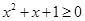 ”; ”; |
B.若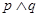 为假命题,则p,q均为假命题; 为假命题,则p,q均为假命题; |
C.若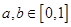 ,则不等式 ,则不等式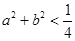 成立的概率是 成立的概率是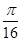 ; ; |
D.“平面向量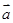 与 与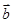 的夹角是钝角”的必要不充分条件是“ 的夹角是钝角”的必要不充分条件是“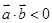 ”. ”. |
设命题 :函数
:函数 在
在 上为增函数;命题
上为增函数;命题 :函数
:函数 为奇函数.则
为奇函数.则
下列命题中真命题是( )
A. |
B. |
C. |
D. |
对于以下判断:
(1)命题“已知 ”,若x
”,若x 2或y
2或y 3,则x+y
3,则x+y 5”是真命题.
5”是真命题.
(2)设f(x)的导函数为f'(x),若f'(x0)=0,则x0是函数f(x)的极值点.
(3)命题“ ,ex﹥0”的否定是:“
,ex﹥0”的否定是:“ ,ex﹥0”.
,ex﹥0”.
(4)对于函数f(x),g(x),f(x) g(x)恒成立的一个充分不必要的条件是f(x)min
g(x)恒成立的一个充分不必要的条件是f(x)min g(x)max.
g(x)max.
其中正确判断的个数是( )
| A.1 | B.2 | C.3 | D.0 |
(本小题满分12分)已知命题 :在
:在 上定义运算
上定义运算 :
: 不等式
不等式 对任意实数
对任意实数 恒成立;命题
恒成立;命题 :若不等式
:若不等式 对任意的
对任意的 恒成立.若
恒成立.若 为假命题,
为假命题, 为真命题,求实数
为真命题,求实数 的取值范围.
的取值范围.