高中数学几何不等式试题

设a，b∈R，定义运算“∧”和“∨”如下：
a∧b＝a∨b＝
若正数a，b，c，d满足ab≥4，c＋d≤4，则(  )

A．a∧b≥2，c∧d≤2	B．a∧b≥2，c∨d≥2
C．a∨b≥2，c∧d≤2	D．a∨b≥2，c∨d≥2

实数a_i（i=1,2,3,4,5,6）满足（a₂－a₁）²+（a₃－a₂）²+（a₄－a₃）²+（a₅－a₄）²+（a₆－a₅）²=1则（a₅+a₆）－（a₁+a₄）的最大值为（　　　）

A．3

B．2

C．

D．1

已知实数a,b,c,d满足a+b=c+d=1,ac+bd>1,求证:a,b,c,d中至少有一个是负数.

小王从甲地到乙地往返的时速分别为a和b(a<b),其全程的平均时速为v,则(　　)

A．a<v<	B．v=
C．<v<	D．v=

某商家一月份至五月份累计销售额达3860万元,预测六月份销售额为500万元,七月份销售额比六月份递增x%,八月份销售额比七月份递增x%,九、十月份销售总额与七、八月份销售总额相等,若一月份至十月份销售总额至少达7000万元,则x的最小值是　　　.

“不等式x²-x+m>0在R上恒成立”的一个必要不充分条件是(　　)

A．m>	B．0<m<1
C．m>0	D．m>1

某公司租赁甲、乙两种设备生产A,B两类产品,甲种设备每天能生产A类产品5件和B类产品10件,乙种设备每天能生产A类产品6件和B类产品20件.已知设备甲每天的租赁费为200元,设备乙每天的租赁费为300元,现该公司要生产A类产品至少50件,B类产品至少140件,所需租赁费最多不超过2500元,写出满足上述所有不等关系的不等式.

设x,y为实数,满足3≤xy²≤8,4≤≤9,则的最大值是　　　　　　.

若不等式的解集为，则实数的值为          .

关于x的不等式x²－2ax－8a²＜0(a＞0)的解集为(x₁，x₂)，且x₂－x₁＝15，则a＝(　　)

A．

B．

C．

D．

在R上定义运算：xy＝x(1－y)．若对任意x>2，不等式(x－a)x≤a＋2都成立，则实数a的取值范围是(　　)

A．[－1，7]	B．(－∞，3]
C．(－∞，7]	D．(－∞，－1]∪[7，＋∞)

“关于的不等式对于一切实数都成立”是“”的

A．充要条件	B．充分非必要条件
C．必要非充分条件	D．既非充分又非必要条件

不等式表示的区域在直线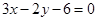的(  )

A．右上方

B．右下方

C．左上方

D．左下方

设f(x)是定义在R上的奇函数，且f(－1)＝0，当x＞0时，(x²＋1)f′(x)－2xf(x)＜0，则不等式f(x)＞0的解集为________．

设，求的值.