有下列六个命题:
(1)一定存在直线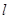 ,使函数
,使函数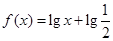 的图像与函数
的图像与函数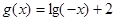 的图像关于直线
的图像关于直线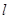 对称;
对称;
(2)直线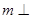 平面
平面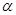 ,直线
,直线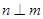 ,则
,则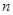 ∥
∥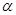 ;
;
(3)已知数列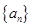 的前
的前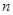 项和为
项和为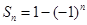 ,
,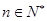 ,则数列
,则数列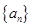 一定是等比数列;
一定是等比数列;
(4)过抛物线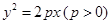 上的任意一点
上的任意一点 的切线方程一定可以表示为
的切线方程一定可以表示为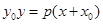 ;
;
(5)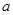 是正数,则“
是正数,则“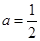 ”是“对任意正数
”是“对任意正数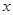 ,
,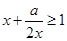 ”的充要条件;
”的充要条件;
(6)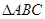 中,
中, ,则
,则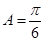 .则正确命题的个数是_______.
.则正确命题的个数是_______.
已知[x]表示不超过实数x的最大整数,如[1.8]=1,[-1.2]=-2.x0是函数f(x)=ln x- 的零点,则[x0]等于________.
的零点,则[x0]等于________.
给出定义:若函数f(x)在D上可导,即f′(x)存在,且导函数f′(x)在D上也可导,则称f(x)在D上存在二阶导函数,记f″(x)=(f′(x))′,若f″(x)<0在D上恒成立,则称f(x)在D上为凸函数.以下四个函数在(0, )上不是凸函数的是________.
)上不是凸函数的是________.
①f(x)=sim x+cos x ②f(x)=ln x-2x
③f(x)=x3+2x-1 ④f(x)=x·ex
设函数 的定义域为D,若存在非零实数m满足对任意
的定义域为D,若存在非零实数m满足对任意  ,均有
,均有 ,且
,且 ,则称
,则称 为
为 上的m高调函数.如果定义域为R的函数
上的m高调函数.如果定义域为R的函数 是奇函数,当x≥0时,
是奇函数,当x≥0时, ,且
,且 为R上的8高调函数,那么实数a的取值范围是 .
为R上的8高调函数,那么实数a的取值范围是 .
一个平面图由若干顶点与边组成,各顶点用一串从1开始的连续自然数进行编号,记各边的编号为它的两个端点的编号差的绝对值,若各条边的编号正好也是一串从1开始的连续自然数,则称这样的图形为“优美图”.已知如图是“优美图”,则点A,B与边a所对应的三个数分别为________.
一般地,如果函数 的定义域为
的定义域为 ,值域也为
,值域也为 ,则称函数
,则称函数 为“保域函数”,下列函数是“保域函数”的有 .(填上所有正确答案的序号)
为“保域函数”,下列函数是“保域函数”的有 .(填上所有正确答案的序号)
① ; ②
; ② ;
;
③ ;④
;④ ;
;
⑤ 。
。
设 表示不超过
表示不超过 的最大整数,如:
的最大整数,如: ,
, .给出下列命题:
.给出下列命题:
①对任意实数 ,都有
,都有 ;
;
②若 ,则
,则 ;
;
③ ;
;
④若函数 ,则
,则 的值域为
的值域为 .
.
其中所有真命题的序号是__________.
对向量a=(a1,a2),b=(b1,b2)定义一种运算“⊗”:a⊗b=(a1,a2)⊗(b1,b2)=(a1b1,a2b2).已知动点P,Q分别在曲线y=sin x和y=f(x)上运动,且 =m⊗
=m⊗ +n(其中O为坐标原点),若向量m=(
+n(其中O为坐标原点),若向量m=( ,3),n=(
,3),n=( ,0),则y=f(x)的最大值为________.
,0),则y=f(x)的最大值为________.
如图,直线l和圆C,当l从l0开始在平面上绕点O按逆时针方向匀速转动(转动角度不超过90°)时,它扫过的圆内阴影部分的面积S是时间t的函数,这个函数的图像大致是________(填序号).

已知R上的不间断函数 满足:(1)当
满足:(1)当 时,
时, 恒成立;(2)对任意的
恒成立;(2)对任意的 都有
都有 。奇函数
。奇函数 满足:对任意的
满足:对任意的 ,都有
,都有 成立,当
成立,当 时,
时, 。若关于
。若关于 的不等式
的不等式 对
对 恒成立,则
恒成立,则 的取值范围 。
的取值范围 。
在实数集 中,我们定义的大小关系“
中,我们定义的大小关系“ ”为全体实数排了一个“序”.类似实数排序的定义,我们定义“点序”记为“
”为全体实数排了一个“序”.类似实数排序的定义,我们定义“点序”记为“ ”:已知
”:已知 和
和 ,
, ,当且仅当“
,当且仅当“ ”或“
”或“ 且
且 ”.定义两点的“
”.定义两点的“ ”与“
”与“ ”运算如下:
”运算如下:
 .
.
则下面四个命题:
①已知 和
和 ,则
,则 ;
;
②已知 和
和 ,若
,若 ,则
,则 ,且
,且 ;
;
③已知 ,
, ,则
,则 ;
;
④已知 ,则对任意的点
,则对任意的点 ,都有
,都有 ;
;
⑤已知 ,则对任意的点
,则对任意的点 ,都有
,都有 .
.
其中真命题的序号为 (把真命题的序号全部写出)