已知函数f (x)="f" (p-x),且当 时,f (x)="x+tan" x,设a="f" (1),b="f" (2),c="f" (3),则 ( )
时,f (x)="x+tan" x,设a="f" (1),b="f" (2),c="f" (3),则 ( )
| A.a<b<c | B.b<c<a | C.c<b<a | D.c<a<b |
如果函数 在区间
在区间 上是增函数,而函数
上是增函数,而函数 在区间
在区间 上是减函数,那么称函数
上是减函数,那么称函数 是区间
是区间 上的“缓增函数”,区间
上的“缓增函数”,区间 叫做“缓增区间”,若函
叫做“缓增区间”,若函 是区间
是区间 上的“缓增函数”,则其“缓增区间”
上的“缓增函数”,则其“缓增区间” 为
为
A. |
B. |
C. |
D. |
若直角坐标平面内的两个不同的点 满足条件:①
满足条件:① 都在函数
都在函数 的图象上;②
的图象上;② 关于原点对称.则称点对
关于原点对称.则称点对 为函数
为函数 的一对“友好点对”.(注:点对
的一对“友好点对”.(注:点对 与
与 为同一“友好点对”).已知函数
为同一“友好点对”).已知函数 ,此函数的友好点对有( )
,此函数的友好点对有( )
| A.0对 | B.1对 | C.2对 | D.3对 |
设函数 的定义域为
的定义域为 ,若函数
,若函数 满足条件:存在
满足条件:存在
 ,使得
,使得 在区间
在区间 上的值域为
上的值域为
 ,则称
,则称 为“
为“ 倍缩函数”,若函数
倍缩函数”,若函数 为“
为“ 倍缩函数”,则
倍缩函数”,则 的取值范围为( )
的取值范围为( )
A. |
B. |
C. |
D. |
【原创】设函数 在
在 上有意义,对给定正数
上有意义,对给定正数 ,定义函数
,定义函数 ,
,
则称函数 为
为 的“孪生函数”,若给定函数
的“孪生函数”,若给定函数 ,
, ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
【原创】已知点 ,点
,点 在曲线
在曲线 上,若线段
上,若线段 与曲线
与曲线 相交且交点恰为线段
相交且交点恰为线段 的中点,则称点
的中点,则称点 为曲线
为曲线 与曲线
与曲线 的一个“相关点”,记曲线
的一个“相关点”,记曲线 与曲线
与曲线 的“相关点”的个数为
的“相关点”的个数为 ,则 ( )
,则 ( )
A. |
B. |
C. |
D. |
对定义在 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数 称为
称为 函数:
函数:
(i)对任意的 ,恒有
,恒有 ;
;
(ii)当 时,总有
时,总有 成立.
成立.
则下列三个函数中不是 函数的个数是( )
函数的个数是( )
① ②
② ③
③
| A.0 | B.1 | C.2 | D.3 |
设函数 在R上有定义,对于任一给定的正数
在R上有定义,对于任一给定的正数 ,定义函数
,定义函数 ,则称函数
,则称函数 为
为 的“
的“ 界函数”若给定函数
界函数”若给定函数 ,则下列结论不成立的是( )
,则下列结论不成立的是( )
A. |
B. |
C. |
D. |
(原题)设函数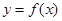 的定义域为
的定义域为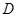 ,如果存在非零常数
,如果存在非零常数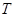 ,对于任意
,对于任意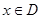 ,都有
,都有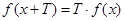 ,则称函数
,则称函数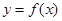 是“似周期函数”,非零常数
是“似周期函数”,非零常数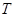 为函数
为函数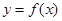 的“似周期”.现有下面四个关于“似周期函数”的命题:
的“似周期”.现有下面四个关于“似周期函数”的命题:
①如果“似周期函数”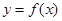 的“似周期”为-1,那么它是周期为2的周期函数;
的“似周期”为-1,那么它是周期为2的周期函数;
②函数 是“似周期函数”;
是“似周期函数”;
③函数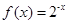 是“似周期函数”;
是“似周期函数”;
④如果函数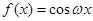 是“似周期函数”,那么“
是“似周期函数”,那么“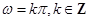 ”.
”.
其中是真命题的序号是 .(写出所有满足条件的命题序号)
(改编)设函数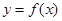 的定义域为
的定义域为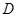 ,如果存在非零常数
,如果存在非零常数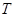 ,对于任意
,对于任意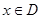 ,都有
,都有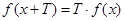 ,则称函数
,则称函数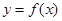 是类周期函数,非零常数
是类周期函数,非零常数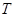 为函数
为函数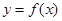 的类周期”.现有下面四个关于类周期函数的命题:
的类周期”.现有下面四个关于类周期函数的命题:
①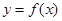 的类周期为-1,那么它是周期为2的周期函数;
的类周期为-1,那么它是周期为2的周期函数;
②若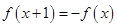 ,则
,则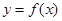 不是类周期函数;
不是类周期函数;
③函数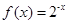 是类周期函数;
是类周期函数;
④如果函数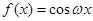 是类周期函数,那么
是类周期函数,那么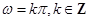 .
.
其中是真命题的有( )
| A.①②④ | B.①③④ | C.②③④ | D.①②③ |
【原创】设函数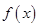 的定义域为
的定义域为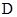 ,如果
,如果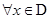 ,
,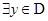 ,使得
,使得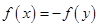 成立,那
成立,那
么称函数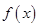 为“
为“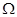 函数”.则下列四个函数中,不属于“
函数”.则下列四个函数中,不属于“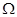 函数”的是( )
函数”的是( )
A.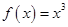 |
B.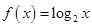 |
C. |
D. |
【原创】集合 由满足:对任意
由满足:对任意 时,都有
时,都有 的函数
的函数 组成.对于两个函数
组成.对于两个函数 ,以下关系成立的是 ( )
,以下关系成立的是 ( )
A. |
B. |
C. |
D. |
对任意的 、
、 ,定义:
,定义: =
= ;
; =
= .则下列各式中
.则下列各式中
恒成立的个数为( )
①
②
③
④
| A.1 | B.2 | C.3 | D.4 |
已知 ,若函数
,若函数 在定义域内的一个区间
在定义域内的一个区间 上函数值的取值范围恰好是
上函数值的取值范围恰好是 ,则称区间
,则称区间 是函数
是函数 的一个减半压缩区间,若函数
的一个减半压缩区间,若函数 存在一个减半压缩区间
存在一个减半压缩区间 ,(
,( ),则实数m的取值范围是( )
),则实数m的取值范围是( )
A. |
B. |
C. |
D. |
定义符号函数  ,则下列结论中错误的是
,则下列结论中错误的是
A. |
B. |
C. |
D. |