高中数学函数迭代选择题

若在曲线f(x,y)=0上存在两个不同点处的切线重合,则称这条切线为曲线f(x,y)=0的“自公切线”.下列方程:①x²-y²=1;②y=x²-|x|;③y=3sinx+4cosx;④|x|+1=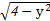对应的曲线中存在“自公切线”的有(　　)

A．①②	B．②③
C．①④	D．③④

已知函数y=f(x)的图象如图,则不等式f(3x-x²)<0的解集为(　　)

A．{x|1<x<2}	B．{x|0<x<3}
C．{x|x<1或x>2}	D．{x|x<0或x>3}

对于函数，若都是某一三角形的三边长，则称为“可构造三角形函数”．以下说法正确的是（   ）

A．不是“可构造三角形函数”；

B．“可构造三角形函数”一定是单调函数；

C．是“可构造三角形函数”；

D．若定义在上的函数的值域是（为自然对数的底数），则一定是“可构造三角形函数”．

函数y＝f(x)，x∈D，若存在常数C，对任意的x₁∈D，存在唯一的x₂∈D使得＝C，则称函数f(x)在D上的几何平均数为C.已知f(x)＝x³，x∈[1,2]，则函数f(x)＝x³在[1,2]上的几何平均数为(　　)

A．	B．2
C．4	D．2

对实数a和b,定义运算“⊗”:a⊗b=设函数f(x)=(x²-1)⊗(x-x²),x∈R.若函数y=f(x)-c恰有两个不同的零点,则实数c的取值范围是(　　)

A．(-∞,-1)∪(-,0)	B．{-1,-}
C．(-1,-)	D．(-∞,-1)∪[-,0)

已知函数f(x)是定义在(0,+∞)上的单调函数,若对任意x∈(0,+∞),都有f(f(x)-)=2,则f()的值是(　　)

A．5

B．6

C．7

D．8

设函数，，则函数的值域为（   ）

A．	B．
C．	D．

已知函数设表示中的较大值,表示中的较小值,记得最小值为得最大值为,则 (      )

A．

B．

C．

D．

已知函数,,设函数，且函数的零点均在区间内，则的最小值为（    ）

A．11

B．10

C．9

D．8

设[x]表示不大于x的最大整数, 则对任意实数x, y, 有（）

A．	$\left[-x\right]=-\left[x\right]$	B．	$\left[2x\right]=2\left[x\right]$
C．	$\left[x+y\right]\le \left[x\right]+\left[y\right]$	D．	$\left[x-y\right]\le \left[x\right]-\left[y\right]$

函数是定义在上的偶函数，且对任意的，都有.当时，.若直线与函数的图象有两个不同的公共点，则实数的值为（       ）

A．	B．
C．或	D．或

函数有两个不同的零点，则实数的取值范围是

A．	B．
C．	D．

设f(x)是定义在R上的偶函数，对x∈R，都有f(x+4)=f(x)，且当x∈[－2,0]时，f(x)＝()^x－1，若在区间(－2，6]内关于x的方程f(x)－log_a(x＋2)＝0(a＞1)恰有3个不同的实数根，则a的取值范围是

A．(1,2)

B．(2，＋∞)

C．(1,)

D．(,2)

函数，,则

A．为偶函数，且在上单调递减

B．为偶函数，且在上单调递增

C．为奇函数，且在上单调递增

D．为奇函数，且在上单调递减

设函数，则满足的的取值范围是（　　）

A．

B．

C．

D．