高中数学函数迭代选择题

一只蚂蚁从正方体的顶点处出发，经正方体的表面，按最短路线爬行到达顶点位置，则下列图形中可以表示正方体及蚂蚁最短爬行路线的正视图是（ ）

A．①②

B．①③

C．③④

D．②④

已知实数满足，则的取值范围是（   ）

A．

B．

C．

D．

若函数对任意且，都有，则称函数为“穿透”函数，则下列函数中，不是“穿透”函数的是(   )

A．

B．

C．

D．

若函数的图象上存在不同两点，设线段的中点为，使得在点处的切线与直线平行或重合，则称切线为函数的“平衡切线”．则函数的“平衡切线”的条数为（   ）

A．条或无数条	B．条或无数条
C．条或无数条	D．条或条

一个函数f（x），如果对任意一个三角形，只要它的三边长a，b，c都在f（x）的定义域内，就有f（a），f（b），f（c）也是某个三角形的三边长，则称f（x）为“三角保型函数”，给出下列函数：①f（x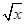）=，②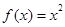；③f（x）=2x；④f（x）=lgx，其中是“三角保型函数”的是（ ）

A．①②

B．①③

C．②③④

D．③④

设与是定义在同一区间上的两个函数，若对任意的，都有，则称和在上是“密切函数”，称为“密切区间”，设与在上是“密切函数”，则它的“密切区间”可以是（    ）

A．

B．

C．

D．

设函数的定义域为，若存在常数，使对一切实数均成立，则称为“倍约束函数”．现给出下列函数：①；②；③；④；⑤是定义在实数集上的奇函数，且对一切，均有．其中是“倍约束函数”的有（   ）

A．1个

B．2个

C．3个

D．4个

定义在上的可导函数，当时，恒成立，若，，，则的大小关系是(   )

A．

B．

C．

D．

定义区间的长度均为．用表示不超过x的最大整数．记，其中．设，若用d表示不等式解集区间的长度，则当时，有(   )

A．

B．

C．

D．

若自然数使得作竖式加法时均不产生进位现象，便称为“好数”．如因为12+13+14不产生进位现象，所以12是“好数”；但 13+14+15产生进位现象，所以13不是“好数”，则不超过100的“好数”共有（  ）

A．9个

B．11个

C．12个

D．15个

规定甲乙两地通话分钟的电话费由（单位：元）给出，其中，记大于或等于的最小整数（如：），若从甲地到乙地通话费用为元，则通话时间的取值范围是（ ）

A．

B．

C．

D．

若函数的最小值为3，则实数的值为（   ）

A．

5或8

B．

或5

C．

或

D．

或8

若函数为定义域上的单调函数，且存在区间(其中)，使得当时，的取值范围恰为，则称函数是上的正函数.若函数是上的正函数，则实数的取值范围为(     )

A．

B．

C．

D．

在R上定义运算，若不等式成立，则实数a的取值范围是(　　)．

A．{a|}	B．{a|}
C．{a|}	D．{a|}

函数y＝，x∈(－π，0)∪(0，π)的图象可能是下列图象中的(　　)