江西省九江市七校高二下学期期中联考文科数学试卷
已知函数 是
是 上的增函数,
上的增函数, 是其图像上的两点,那么
是其图像上的两点,那么 的解集为( )
的解集为( )
A. |
B. |
C. |
D. |
下表是降耗技术改造后生产甲产品过程中记录的产量 (吨)与相应的生产能耗
(吨)与相应的生产能耗 (吨标准煤)的几组对应数据,根据表中提供的数据,求出
(吨标准煤)的几组对应数据,根据表中提供的数据,求出 关于
关于 的线性回归方程:
的线性回归方程: ,那么表中
,那么表中 的值为( )
的值为( )
| A.3 | B.3.15 | C.4.5 | D.4 |
用反证法证明命题:“若
 ,那么
,那么 ,
, ,
, 中至少有一个不小于
中至少有一个不小于 ”时,反设正确的是( )
”时,反设正确的是( )
A.假设 , , , , 至多有两个小于 至多有两个小于 |
B.假设 , , , , 至多有一个小于 至多有一个小于 |
C.假设 , , , , 都不小于 都不小于 |
D.假设 , , , , 都小于 都小于 |
将自然数0,1,2,按照如下形式进行摆列:
根据以上规律判定,从2012到2014的箭头方向是( )



已知 是定义在
是定义在 上的偶函数,且
上的偶函数,且 ,若
,若 在
在 上单调递减,则
上单调递减,则 在
在 上是( )
上是( )
| A.增函数 | B.减函数 | C.先增后减的函数 | D.先减后增的函数 |
已知图①中的图像对应的函数为 ,则图②的图像对应的函数为( )
,则图②的图像对应的函数为( )
A. |
B. |
C. |
D. |
若函数 为定义域
为定义域 上的单调函数,且存在区间
上的单调函数,且存在区间 (其中
(其中 ),使得当
),使得当 时,
时, 的取值范围恰为
的取值范围恰为 ,则称函数
,则称函数 是
是 上的正函数.若函数
上的正函数.若函数 是
是 上的正函数,则实数
上的正函数,则实数 的取值范围为( )
的取值范围为( )
A. |
B. |
C. |
D. |
设 的三边长分别为
的三边长分别为 ,
, 的面积为
的面积为 ,内切圆半径为
,内切圆半径为 ,则
,则 ;类比这个结论可知:四面体
;类比这个结论可知:四面体 的四个面的面积分别为
的四个面的面积分别为 ,内切球的半径为
,内切球的半径为 ,四面体
,四面体 的体积为
的体积为 ,则
,则 .
.
下列四个命题中,真命题的序号有 .(写出所有真命题的序号)
①若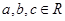 ,则“
,则“ ”是“
”是“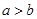 ”成立的充分不必要条件;
”成立的充分不必要条件;
②命题“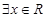 使得
使得 ”的否定是“
”的否定是“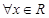 均有
均有 ”;
”;
③命题“若 ,则
,则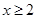 或
或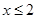 ”的否命题是“若
”的否命题是“若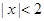 ,则
,则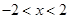 ”;
”;
④函数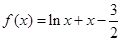 在区间
在区间 上有且仅有一个零点.
上有且仅有一个零点.
为了解某班学生喜爱打篮球是否与性别有关,对本班 人进行了问卷调查得到了如下的列联表:
人进行了问卷调查得到了如下的列联表:
| |
喜爱打篮球 |
不喜爱打篮球 |
合计 |
| 男生 |
|
5 |
|
| 女生 |
10 |
|
|
| 合计 |
|
|
50 |
已知在全部 人中随机抽取1人抽到喜爱打篮球的学生的概率为
人中随机抽取1人抽到喜爱打篮球的学生的概率为 .
.
(1)请将上面的列联表补充完整(不用写计算过程);
(2)能否认为喜爱打篮球与性别有关?说明你的理由.(参考公式: ,其中
,其中 )
)
将一颗质地均匀的正四面体骰子(四个面的点数分别为1,2,3,4)先后抛掷两次,记第一次出现的点数为 ,第二次出现的点数为
,第二次出现的点数为 .
.
(1)记事件 为“
为“ ”,求
”,求 ;
;
(2)记事件 为“
为“ ”,求
”,求 .
.
 等于( )
等于( )



 ,则阴影部分表示的集合为( )
,则阴影部分表示的集合为( )




 ,则下列推证中正确的是( )
,则下列推证中正确的是( )



 ,且
,且 ,则
,则 等于 .
等于 . 的范围是
的范围是 ,则输入实数
,则输入实数 的范围应是 .
的范围应是 .
 对任意实数
对任意实数 恒成立,则正实数
恒成立,则正实数 的取值范围 .
的取值范围 . ,
, .
. 时,求
时,求 和
和 ;
; ,求实数
,求实数 的取值范围.
的取值范围. ,
, ,若
,若 是
是 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围. ,求证
,求证 ;
; ,求证:
,求证: .
. 满足对任意的
满足对任意的 恒有
恒有 ,且当
,且当 时,
时, .
. 的值;
的值; ,解不等式
,解不等式 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号