若 满足
满足 ,则称
,则称 为
为 的不动点.
的不动点.
(1)若函数 没有不动点,求实数
没有不动点,求实数 的取值范围;
的取值范围;
(2)若函数 的不动点
的不动点 ,求
,求 的值;
的值;
(3)若函数 有不动点,求实数
有不动点,求实数 的取值范围.
的取值范围.
若函数 的图象上存在不同两点
的图象上存在不同两点 ,设线段
,设线段 的中点为
的中点为 ,使得
,使得 在点
在点 处的切线
处的切线 与直线
与直线 平行或重合,则称切线
平行或重合,则称切线 为函数
为函数 的“平衡切线”.则函数
的“平衡切线”.则函数 的“平衡切线”的条数为()
的“平衡切线”的条数为()
A. 条或无数条 条或无数条 |
B. 条或无数条 条或无数条 |
C. 条或无数条 条或无数条 |
D. 条或 条或 条 条 |
(原题)设函数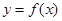 的定义域为
的定义域为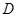 ,如果存在非零常数
,如果存在非零常数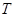 ,对于任意
,对于任意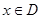 ,都有
,都有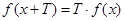 ,则称函数
,则称函数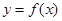 是“似周期函数”,非零常数
是“似周期函数”,非零常数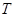 为函数
为函数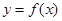 的“似周期”.现有下面四个关于“似周期函数”的命题:
的“似周期”.现有下面四个关于“似周期函数”的命题:
①如果“似周期函数”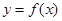 的“似周期”为-1,那么它是周期为2的周期函数;
的“似周期”为-1,那么它是周期为2的周期函数;
②函数 是“似周期函数”;
是“似周期函数”;
③函数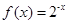 是“似周期函数”;
是“似周期函数”;
④如果函数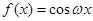 是“似周期函数”,那么“
是“似周期函数”,那么“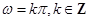 ”.
”.
其中是真命题的序号是 .(写出所有满足条件的命题序号)
(改编)设函数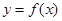 的定义域为
的定义域为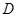 ,如果存在非零常数
,如果存在非零常数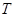 ,对于任意
,对于任意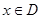 ,都有
,都有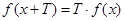 ,则称函数
,则称函数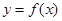 是类周期函数,非零常数
是类周期函数,非零常数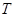 为函数
为函数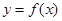 的类周期”.现有下面四个关于类周期函数的命题:
的类周期”.现有下面四个关于类周期函数的命题:
①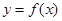 的类周期为-1,那么它是周期为2的周期函数;
的类周期为-1,那么它是周期为2的周期函数;
②若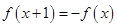 ,则
,则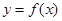 不是类周期函数;
不是类周期函数;
③函数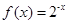 是类周期函数;
是类周期函数;
④如果函数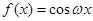 是类周期函数,那么
是类周期函数,那么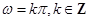 .
.
其中是真命题的有()
| A.①②④ | B.①③④ | C.②③④ | D.①②③ |
一个函数f(x),如果对任意一个三角形,只要它的三边长a,b,c都在f(x)的定义域内,就有f(a),f(b),f(c)也是某个三角形的三边长,则称f(x)为“三角保型函数”,给出下列函数:①f(x)=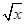 ,②
,②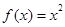 ;③f(x)=2x;④f(x)=lgx,其中是“三角保型函数”的是()
;③f(x)=2x;④f(x)=lgx,其中是“三角保型函数”的是()
| A.①② | B.①③ | C.②③④ | D.③④ |
设函数 在
在 上的最小值为
上的最小值为 ,最大值为
,最大值为 若存在最小正整数
若存在最小正整数 使得
使得
 对任意
对任意 成立,则称函数
成立,则称函数 为区间
为区间 上的“
上的“ 阶
阶 函数”若函数
函数”若函数 为区间
为区间 上的“
上的“ 阶
阶 函数”,则
函数”,则 的值为()
的值为()
| A.4 | B.3 | C.2 | D.1 |
设函数 的定义域为
的定义域为 ,若存在常数
,若存在常数 ,使
,使 对一切实数
对一切实数 均成立,则称
均成立,则称 为“倍约束函数”.现给出下列函数:①
为“倍约束函数”.现给出下列函数:① ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ 是定义在实数集
是定义在实数集 上的奇函数,且对一切
上的奇函数,且对一切 ,
, 均有
均有 .其中是“倍约束函数”的有()
.其中是“倍约束函数”的有()
| A.1个 | B.2个 | C.3个 | D.4个 |
【原创】设函数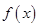 的定义域为
的定义域为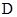 ,如果
,如果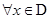 ,
,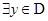 ,使得
,使得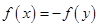 成立,那
成立,那
么称函数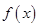 为“
为“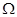 函数”.则下列四个函数中,不属于“
函数”.则下列四个函数中,不属于“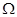 函数”的是()
函数”的是()
A.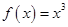 |
B.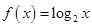 |
C. |
D. |
若在定义域内存在实数x0,使得f(x0+1)=f(x0)+f(1)成立,则称函数f(x)是“可拆函数”.
(1)函数f(x)= 是否是“可拆函数”?请说明理由;
是否是“可拆函数”?请说明理由;
(2)若函数f(x)=2x+b+2x是“可拆函数”,求实数b的取值范围:
(3)证明:f(x)=cosx是“可拆函数”.
设函数 在
在 上有定义,对于任一给定的正数
上有定义,对于任一给定的正数 ,定义函数
,定义函数 ,则称函数
,则称函数 为
为 的“
的“ 界函数”,若给定函数
界函数”,若给定函数 ,则下列结论不成立的是: .
,则下列结论不成立的是: .
① ;
;
② ;
;
③ ;
;
④
对于任意x,[x]表示不超过x的最大整数,如[1.1]=1,[﹣2.1]=﹣3,定义R上的函数f(x)=[2x]+[4x]+[8x],若A={y|y=f(x),0≤x≤1},则A中所有元素的和为()
| A.55 | B.58 | C.63 | D.65 |
对于任意实数x,符号 [x]表示不超过x的最大整数(如[-1.5]=-2,[0]=0,[2.3]=2),则 的值为 ()
的值为 ()
| A.0 | B.-2 | C.-1 | D.1 |
已知函数f (x)="f" (p-x),且当 时,f (x)="x+tan" x,设a="f" (1),b="f" (2),c="f" (3),则 ()
时,f (x)="x+tan" x,设a="f" (1),b="f" (2),c="f" (3),则 ()
| A.a<b<c | B.b<c<a | C.c<b<a | D.c<a<b |