已知函数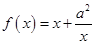 ,
,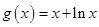 ,其中
,其中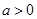 .
.
(1)若 是函数
是函数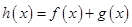 的极值点,求实数
的极值点,求实数 的值;
的值;
(2)若对任意的 (
(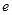 为自然对数的底数)都有
为自然对数的底数)都有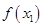 ≥
≥ 成立,求实数
成立,求实数 的取值范围.
的取值范围.
设函数 ,观察:
,观察: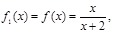
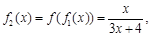

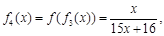
……根据以上事实,由归纳推理可得:
当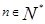 且
且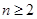 时,
时,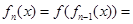 .
.
已知函数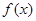 的定义域为
的定义域为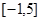 ,部分对应值如下表。
,部分对应值如下表。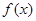 的导函数
的导函数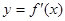 的图像如图所示。
的图像如图所示。
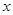 |
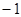 |
0 |
 |
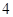 |
 |
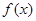 |
 |
 |
 |
 |
 |
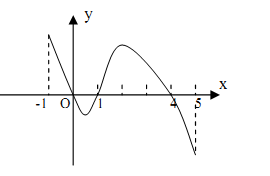
下列关于函数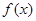 的命题:
的命题:
①函数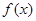 在
在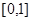 上是减函数;②如果当
上是减函数;②如果当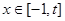 时,
时,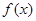 最大值是
最大值是 ,那么
,那么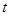 的最大值为
的最大值为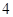 ;③函数
;③函数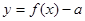 有
有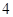 个零点,则
个零点,则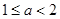 ;④已知
;④已知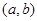 是
是 的一个单调递减区间,则
的一个单调递减区间,则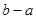 的最大值为
的最大值为 。
。
其中真命题的个数是( )
A、4个 B、3个 C、2个 D、1个
若函数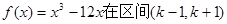 上不是单调函数,则实数k的取值范围是( )
上不是单调函数,则实数k的取值范围是( )
A. |
B.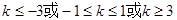 |
C. |
D.不存在这样的实数k |
已知函数 是R上的奇函数,若对于
是R上的奇函数,若对于 ,都有
,都有 ,
, 时,
时, 的值为( )
的值为( )
A. |
B. |
C.1 | D.2 |
设 是定义域为
是定义域为 ,最小正周期为
,最小正周期为 的函数。若
的函数。若 , 则
, 则 等于( )
等于( )
| A.1 | B. |
C.0 | D. |
已知定义在 上的函数
上的函数 ,对任意的
,对任意的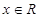 ,都有
,都有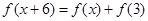 成立,若函数
成立,若函数 的图象关于直线
的图象关于直线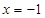 对称,则
对称,则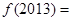
A. |
B.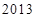 |
C. |
D. |
已知函数 ,
, (其中
(其中 ).
).
(Ⅰ)求函数 的极值;
的极值;
(Ⅱ)若函数 在区间
在区间 内有两个零点,求正实数a的取值范围;(Ⅲ)求证:当
内有两个零点,求正实数a的取值范围;(Ⅲ)求证:当 时,
时, .(说明:e是自然对数的底数,e=2.71828…)
.(说明:e是自然对数的底数,e=2.71828…)