高中数学一阶、二阶线性常系数递归数列的通项公式选择题

在数列{a_n}中，a_n＋1＝ca_n(c为非零常数)，前n项和为S_n＝3ⁿ＋k，则实数k的值为(　　)

A．－1	B．0
C．1	D．2

如果正整数a的各位数字之和等于6，那么称a为“好数”(如：6,24,2 013等均为“好数”)，将所有“好数”从小到大排成一列a₁，a₂，a₃，…，若a_n＝2 013，则n＝(　　)

A．50	B．51
C．52	D．53

如图所示，当n≥2时，将若干点摆成三角形图案，每条边(包括两个端点)有n个点，若第n个图案中总的点数记为a_n，则a₁＋a₂＋a₃＋…＋a₁₀＝(　　)

A．126	B．135
C．136	D．140

已知曲线C：y＝ (x>0)及两点A₁(x_1,0)和A₂(x_2,0)，其中x₂>x₁>0.过A₁，A₂分别作x轴的垂线，交曲线C于B₁，B₂两点，直线B₁B₂与x轴交于点A₃(x_3,0)，那么(　　)

A．x1，，x2成等差数列	B．x1，，x2成等比数列
C．x1，x3，x2成等差数列	D．x1，x3，x2成等比数列

S_n是数列{a_n}的前n项和，则“S_n是关于n的二次函数”是“数列{a_n}为等差数列”的(　　)

A．充分不必要条件	B．必要不充分条件
C．充分必要条件	D．既不充分也不必要条件

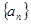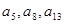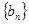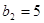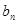数列是公差不为零的等差数列，并且是等比数列的相邻三项，若，则等于（   ）

A．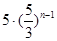

B．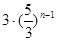

C．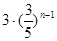

D．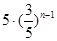

若数列{a_n}满足＝d(n∈N^*，d为常数)，则称数列{a_n}为“调和数列”．已知正项数列为“调和数列”，且b₁＋b₂＋…＋b₉＝90，则b₄·b₆的最大值是(　　)．

A．10

B．100

C．200

D．400

已知数列{a_n}满足a_n＋1＝＋，且a₁＝，则该数列的前2 013项的和等于(　　)．

A．

B．3019

C．1508

D．013

已知数列{a_n}的通项公式是a_n＝，若前n项和为10，则项数n为(　　)．

A．11

B．99

C．120

D．121

已知数列{a_n}的通项公式是a_n＝－n²＋12n－32，其前n项和是S_n，对任意的m，n∈N^*且m<n，则S_n－S_m的最大值是(　　)．

A．－21

B．4

C．8

D．10

已知数列{a_n}满足 且，则的值是(　　)

A．－5

B．－

C．5

D．

设数列的前n项和为，若，则     （    ）

A．

B．

C．

D．

已知数列的前项和，则=(    )

A．36

B．35

C．34

D．33

若数列的通项为，则其前项和为（    ）

A．	B．
C．	D．

已知数列的前项和为，则=      ．