数列{an}满足an+an+1= (n∈N*),且a1=1,Sn是数列{an}的前n项和,则S21=( )
(n∈N*),且a1=1,Sn是数列{an}的前n项和,则S21=( )
A. |
B.6 |
| C.10 | D.11 |
已知等差数列 的公差为
的公差为 ,且
,且 ,若
,若 ,则
,则 为
为
| A.12 | B.10 | C.8 | D.4 |
定义:在数列{an}中,若满足-=d(n∈N*,d为常数),我们称{an}为“比等差数列”.已知在“比等差数列”{an}中,a1=a2=1,a3=2,则的个位数字是( )
| A.3 | B.4 | C.6 | D.8 |
将正偶数集合{2,4,6,…}从小到大按第 组有
组有 个偶数进行分组,{2},{4,6,8} ,{10,12,14,16,18},…第一组、第二组、第三组,则2010位于第 组。( )
个偶数进行分组,{2},{4,6,8} ,{10,12,14,16,18},…第一组、第二组、第三组,则2010位于第 组。( )
| A.30 | B.31 | C.32 | D.33 |
已知 是首项为1的等比数列,
是首项为1的等比数列, 是
是 的前n项和,且
的前n项和,且 ,则数列
,则数列 的前5项和为
的前5项和为
A. 或5 或5 |
B. 或5 或5 |
C. |
D. |
由公差 的等差数列{an}中的项组成一个新数列
的等差数列{an}中的项组成一个新数列 ,
,  ,
, ,…,则下列说法正确的是
,…,则下列说法正确的是
| A.该数列不是等差数列 | B.该数列是公差为 的等差数列 的等差数列 |
C.该数列是公差为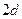 的等差数列 的等差数列 |
D.该数列是公差为 的等差数列 的等差数列 |