(本小题满分14分)已知函数 ,其中
,其中
(1)若 在区间
在区间 上有零点,求实数
上有零点,求实数 的取值范围;
的取值范围;
(2)设函数 ,是否存在实数
,是否存在实数 ,对任意给定的非零实数
,对任意给定的非零实数 ,存在唯一的非零实数
,存在唯一的非零实数 ,使得
,使得 ?若存在,求出
?若存在,求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
已知函数f(x)= ,若存在实数a,b,c,d,满足f(a)=f(b)=f(c)=f(d),其中0<a<b<c<d,则abcd的取值范围 .
,若存在实数a,b,c,d,满足f(a)=f(b)=f(c)=f(d),其中0<a<b<c<d,则abcd的取值范围 .
函数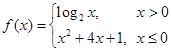 ,若实数
,若实数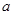 满足
满足 =1,则实数
=1,则实数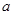 的所有取值的和为( )
的所有取值的和为( )
| A.1 | B. |
C. |
D.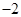 |
关于 的方程
的方程 ,给出下列四个命题:
,给出下列四个命题:
①存在实数 ,使得方程恰有2个不同的实根
,使得方程恰有2个不同的实根
②存在实数 ,使得方程恰有4个不同的实根
,使得方程恰有4个不同的实根
③存在实数 ,使得方程恰有5个不同的实根
,使得方程恰有5个不同的实根
④存在实数 ,使得方程恰有8个不同的实根
,使得方程恰有8个不同的实根
其中假命题的个数是( )
| A.0 | B.1 | C.2 | D.3 |
已知定义在R上的函数 且
且 .若方程
.若方程 有三个不相等的实数根,则实数k的取值范围是( )
有三个不相等的实数根,则实数k的取值范围是( )
A. |
B. |
C. |
D. |