(本小题满分12分)
设函数f(x)=a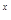 -(k-1)a
-(k-1)a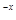 (a>0,a
(a>0,a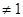 )是定义域为R的奇函数
)是定义域为R的奇函数
(Ⅰ)若f(1)>0,试求使不等式f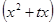 +f
+f >0在定义域上恒成立的t的取值范围
>0在定义域上恒成立的t的取值范围
(Ⅱ)若f(1)=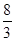 ,且g(x)=a
,且g(x)=a +a
+a -2mf(x)在
-2mf(x)在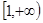 上的最小值为-2,求m的值.
上的最小值为-2,求m的值.
(本小题满分16分)已知函数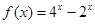 ,实数
,实数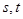 满足
满足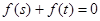 ,设
,设 .
.
(1)当函数 的定义域为
的定义域为 时,求
时,求 的值域;
的值域;
(2)求函数关系式 ,并求函数
,并求函数 的定义域;
的定义域;
(3)求 的取值范围.
的取值范围.
已知函数
 ,函数
,函数 .
.
(1)求函数 与
与 的解析式,并求出
的解析式,并求出 ,
, 的定义域;
的定义域;
(2)设 ,试求函数
,试求函数 的最值.
的最值.
本题共有2个小题,第1小题满分6分,第2小题满分8分
已知函数 .
.
(1)若 为偶函数,求
为偶函数,求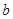 的值;
的值;
(2)若 在区间
在区间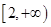 上是增函数,试求
上是增函数,试求 、
、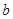 应满足的条件.
应满足的条件.
(本小题满分12分)已知函数 ,函数
,函数 的最小值为
的最小值为 .
.
(1)求 ;
;
(2)是否存在实数m,n同时满足下列条件:
①
②当 的定义域为
的定义域为 时,值域为
时,值域为 ?若存在,求出m,n的值;若不存在,说明理由.
?若存在,求出m,n的值;若不存在,说明理由.
(本小题满分14分)已知函数 .
.
(1)求 的定义域;
的定义域;
(2)在函数 的图像上是否存在不同的两点,使过此两点的直线平行于
的图像上是否存在不同的两点,使过此两点的直线平行于 轴;
轴;
(3)当 满足什么关系时,
满足什么关系时, 在
在 上恒取正值.
上恒取正值.
已知 ,
,
(1)若f(x)的最小值记为h(a),求h(a)的解析式.
(2)是否存在实数m,n同时满足以下条件:① ;②当h(a)的定义域为[n,m]时,值域为[n2,m2];若存在,求出m,n的值;若不存在,说明理由.
;②当h(a)的定义域为[n,m]时,值域为[n2,m2];若存在,求出m,n的值;若不存在,说明理由.
定义在[-1,1]上的奇函数f(x),已知当x∈[-1,0]时,
f(x)= -
- (a∈R).
(a∈R).
(1)求f(x)在[0,1]上的最大值;
(2)若f(x)是[0,1]上的增函数,求实数a的取值范围.
已知函数f(x)=3x- .
.
(1)若f(x)=2,求x的值;
(2)判断x>0时,f(x)的单调性;
(3)若3tf(2t)+mf(t)≥0对于t∈ 恒成立,求m的取值范围.
恒成立,求m的取值范围.