设 和
和 为不重合的两个平面,给出下列命题:
为不重合的两个平面,给出下列命题:
(1)若 内的两条相交直线分别平行于
内的两条相交直线分别平行于 内的两条直线,则
内的两条直线,则 平行于
平行于 ;
;
(2)若 外一条直线
外一条直线 与
与 内的一条直线平行,则
内的一条直线平行,则 和
和 平行;
平行;
(3)设 和
和 相交于直线
相交于直线 ,若
,若 内有一条直线垂直于
内有一条直线垂直于 ,则
,则 和
和 垂直;
垂直;
(4)直线 与
与 垂直的充分必要条件是
垂直的充分必要条件是 与
与 内的两条直线垂直.
内的两条直线垂直.
上面命题中,真命题的序号 (写出所有真命题的序号).
已知直线l⊥平面α,直线m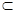 平面β,有下列四个命题:①若α∥β,则l⊥m ;②若α⊥β,则l∥m;③若l∥m,则α⊥β;④若l⊥m,则α∥β.其中正确命题序号是 .
平面β,有下列四个命题:①若α∥β,则l⊥m ;②若α⊥β,则l∥m;③若l∥m,则α⊥β;④若l⊥m,则α∥β.其中正确命题序号是 .
设 和
和 为不重合的两个平面,给出下列命题:
为不重合的两个平面,给出下列命题:
(1)若 内的两条相交直线分别平行于
内的两条相交直线分别平行于 内的两条直线,则
内的两条直线,则 平行于
平行于 ;
;
(2)若 外一条直线
外一条直线 与
与 内的一条直线平行,则
内的一条直线平行,则 和
和 平行;
平行;
(3)设 和
和 相交于直线
相交于直线 ,若
,若 内有一条直线垂直于
内有一条直线垂直于 ,则
,则 和
和 垂直;
垂直;
(4)直线 与
与 垂直的充分必要条件是
垂直的充分必要条件是 与
与 内的两条直线垂直.
内的两条直线垂直.
上面命题中,真命题的序号 (写出所有真命题的序号).
如图是一几何体的平面展开图,其中ABCD为正方形,E,F分别为PA,PD的中点,在此几何体中,给出下面四个结论:
①直线BE与直线CF异面;
②直线BE与直线AF异面;
③直线EF∥平面PBC;
④平面BCE⊥平面PAD.
其中正确的有__________.
如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M为线段PB的中点.有以下四个命题:
①PA∥平面MOB;
②MO∥平面PAC;
③OC⊥平面PAC;
④平面PAC⊥平面PBC.
其中正确的命题是 (填上所有正确命题的序号)
设m,n是两条不同的直线,α、β、γ是三个不同的平面,给出下列四个命题:
(1)若m⊥α,n∥α,则m⊥n
(2)若α∥β,β∥γ,m⊥α,则m⊥γ
(3)若m∥α,n∥α,则m∥n
(4)若α⊥γ,β⊥γ,则α∥β
其中真命题的序号是 .
下图是一个正三棱柱(以 为底面)被一平面所截得到的几何体,截面为
为底面)被一平面所截得到的几何体,截面为 .已知
.已知 ,
, ,
, ,
, .
.
(1)设点 是
是 的中点,证明:
的中点,证明: 平面
平面 ;
;
(2)求 与平面
与平面 所成的角的正弦值;
所成的角的正弦值;
设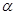 、
、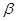 、
、 是三个不同的平面,
是三个不同的平面,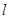 、
、 、
、 是三条不同的直线,则
是三条不同的直线,则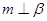 的一个充分条件为 .
的一个充分条件为 .
① ;
;
②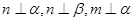 ;
;
③ ;
;
④ .
.
已知正四棱锥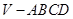 可绕着
可绕着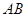 任意旋转,
任意旋转, 平面
平面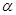 ,若
,若 ,
, ,则正四棱锥
,则正四棱锥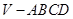 在面
在面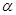 内的投影面积的取值范围是________.
内的投影面积的取值范围是________.
如图是一正方体的表面展开图,B、N、Q都是所在棱的中点,则在原正方体中,①AB与CD相交;②MN∥PQ;③AB∥PE;④MN与CD异面;⑤MN∥平面PQC.
其中真命题的是________(填序号).