如图,在四棱锥P﹣ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(1)证明:PA∥平面EDB;
(2)证明:PB⊥平面EFD.
下列四个正方体图形中, 为正方体的两个顶点,
为正方体的两个顶点, 分别为其所在棱的中点,能得出
分别为其所在棱的中点,能得出 平面
平面 的图形的序号是( )
的图形的序号是( )

| A.①③ | B.②③ | C.①④ | D.②④ |
在空间,下列命题中正确的是 ( )
| A.没有公共点的两条直线平行 |
| B.与同一直线垂直的两条直线平行 |
| C.平行于同一直线的两条直线平行 |
D.已知直线 不在平面 不在平面 内,则直线 内,则直线 平面 平面 |
已知E是矩形ABCD(如图1)边CD上的一点,现沿AE将△DAE折起至△D1AE(如图2),并且平面D1AE⊥平面ABCE,图3为四棱锥D1—ABCE的主视图与左视图.

(1)求证:直线BE⊥平面D1AE;
(2)求点A到平面D1BC的距离.
设m,n,l为空间不重合的直线, 为空间不重合的平面,则下列命题中真命题的序号是 .
为空间不重合的平面,则下列命题中真命题的序号是 .
(1)m//l,n//l,则m//n;
(2)m l,n
l,n l,则m//n;
l,则m//n;
(3) ,则
,则 ;
;
(4) ,则
,则 ;
;
设 为不同的直线,
为不同的直线, 为不同的平面,有如下四个命题:
为不同的平面,有如下四个命题:
①若 ,
, ⊥
⊥ ,则
,则 ∥
∥
②若 ,
,

 ,则
,则 ⊥
⊥
③若 ⊥
⊥ ,
, ⊥
⊥ ,则
,则 ∥
∥
④若 ⊥
⊥ ,
, ∥
∥ 且
且 ∥
∥ ,则
,则 ⊥
⊥
其中正确命题的个数是
| A.1 | B.2 | C.3 | D.4 |
在空间,下列命题错误的是( )
| A.一条直线与两个平行平面中的一个相交,则必与另一个相交 |
| B.一个平面与两个平行平面相交,交线平行 |
| C.平行于同一平面的两个平面平行 |
| D.平行于同一直线的两个平面平行 |
如图,三棱柱 中,侧棱
中,侧棱 底面
底面 ,底面三角形
,底面三角形 是正三角形,
是正三角形, 是
是 中点,则下列叙述正确的是
中点,则下列叙述正确的是
A. 与 与 是异面直线 是异面直线 |
B. 平面 平面 |
C. , , 为异面直线,且 为异面直线,且 |
D. 平面 平面 |
若直线 不平行于平面
不平行于平面 ,且
,且 ,则下列结论成立的是( )
,则下列结论成立的是( )
A. 内的所有直线与 内的所有直线与 异面 异面 |
B. 内不存在与 内不存在与 平行的直线 平行的直线 |
C. 内存在唯一的直线与 内存在唯一的直线与 平行 平行 |
D. 内的直线与 内的直线与 都相交 都相交 |
已知 是空间中两不同直线,
是空间中两不同直线, 是空间中两不同平面,下列命题中正确的是( )
是空间中两不同平面,下列命题中正确的是( )
A.若直线 , , ,则 ,则 |
B.若平面 , , ,则 ,则 |
C.若平面 , , ,则 ,则 |
D.若 , , ,则 ,则 |
如图,在正四棱锥 中,
中, ,
, ,
, 分别是
分别是 ,
, ,
, 的中点,动点
的中点,动点 在线段
在线段 上运动时,下列四个结论:①
上运动时,下列四个结论:① ;②
;② ;③
;③ ;④
;④ .中恒成立的为( )
.中恒成立的为( )
| A.①③ | B.③④ | C.①② | D.②③④ |
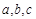 表示直线,
表示直线, 表示平面,下列命题正确的是( )
表示平面,下列命题正确的是( )
A.若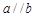 , ,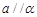 ,则 ,则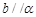 |
B.若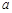 ⊥ ⊥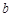 , , 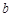 ⊥ ⊥ ,则 ,则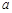 ⊥ ⊥ |
C.若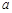 ⊥ ⊥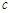 , ,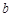 ⊥ ⊥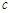 ,则 ,则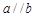 |
D.若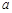 ⊥ ⊥ , ,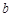 ⊥ ⊥ ,则 ,则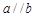 |
若直线 和 是异面直线, 在平面 内, 在平面 内, 是平面 与平面 的交线,则下列命题正确的是( )
| A. | 至少与 中的一条相交 |
| B. | 与 都相交 |
| C. | 至多与 中的一条相交 |
| D. | 与 都不相交 |
已知直线l∥平面α,直线m Ìα,则直线l和m的位置关系是 .
(平行、相交、异面三种位置关系中选)