在用样本频率估计总体分布的过程中,下列说法正确的是
| A.总体容量越大,估计越精确 | B.总体容量越小,估计越精确 |
| C.样本容量越大,估计越精确 | D.样本容量越小,估计越精确 |
下图是样本容量为200的频率分布直方图。根据样本的频率分布直方图估计,样本数据落在 [6,10)内的频数为 ,数据落在[2,10)内的概率约为 。
下列说法中,正确的是 ( )
| A.数据4、6、6、7、9、4的众数是4 |
| B.一组数据的标准差是这组数据的方差的平方 |
| C.数据3,5,7,9的标准差是数据6、10、14、18的标准差的一半 |
| D.频率分布直方图中各小长方形的面积等于相应各组的频数 |
(本题12分)根据空气质量指数API(为整数)的不同,可将空气质量分级如下表:

对某城市一年(365天)的空气质量进行监测,获得的API数据按照区间 ,
, ,
, ,
, ,
, ,
, 进行分组,得到频率分布直方图如图.
进行分组,得到频率分布直方图如图.
(1)求直方图中 的值;
的值;
(2)计算一年中空气质量为良的天数;
(3)某环保部门准备在一年内随机到该城市考察两次空气质量,求两次考察空气质量都为良的概率(结果用分数表示).
为了了解某校今年准备报考飞行员的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为 ,第2个小组的频数为12,则抽取的学生人数是
,第2个小组的频数为12,则抽取的学生人数是
.
某班有50名学生,在一次考试中,统计数学平均成绩为70分,方差为102。后来发现2名同学的成绩有误,甲实得80分却记为50分,乙实得60分却记为90分。更正后平均成绩和方差分别为
| A.70,90 | B.70,114 | C.65,90 | D.65,114 |
某班 名学生在一次百米测试中,成绩全部介于
名学生在一次百米测试中,成绩全部介于 秒与
秒与 秒之间,将测
秒之间,将测 试结果按如下方式分成五组:第一组
试结果按如下方式分成五组:第一组 ,第二组
,第二组 ,…,第五组
,…,第五组 ,下图是按上述分组方法得到的频率分布直方图。
,下图是按上述分组方法得到的频率分布直方图。
(1)若成绩大于或等于 秒且小于
秒且小于 秒认为良好,求该班在这次百米测试中成绩良好的人数;
秒认为良好,求该班在这次百米测试中成绩良好的人数;
(2)若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值大于 的概率。
的概率。
(本小题共13分)
为了调查某厂2000名工人生产某种产品的能力,随机抽查了 位工人某天生产该产品的数量,产品数量的分组区间为
位工人某天生产该产品的数量,产品数量的分组区间为 ,
, ,
, ,
, ,
, ,频率分布直方图如图所示.已知生产的产品数量在
,频率分布直方图如图所示.已知生产的产品数量在 之间的工人有6位.
之间的工人有6位.
(Ⅰ)求 ;
;
(Ⅱ)工厂规定从生产低于20件产品的工人中随机的选取2位工人进行培训,则这2位工
人不在同一组的概率是多少?
甲、乙、丙三名射击运动员在某次测试中各射击20次,三人的测试成绩如下表
|
|
|
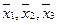 分别表示甲、乙、丙三名运动员的这次测试成绩的平均数,则
分别表示甲、乙、丙三名运动员的这次测试成绩的平均数,则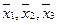 的大小关系是 ;
的大小关系是 ; 分别表示甲、乙、丙三名运动员的这次测试成绩的标准差,则
分别表示甲、乙、丙三名运动员的这次测试成绩的标准差,则 的大小关系是 .
的大小关系是 .
一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如下图),为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出200人作进一步调查,其中低于1500元的称为低收入者,高于3000元的称为高收入者,则应在低收入者和高收入者中分别抽取的人数是( )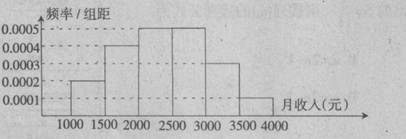
| A.1000,2000 | B.40,80 | C.20,40 | D.10,20 |
为了让学生了解更多“奥运会”知识,某中学举行了一次“奥运知识竞赛”,共有800名学生参加了这次竞赛,为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计。请你根据表中信息解答下列问题:
(1)若用系统抽样的方法抽取容量为50的一个样本,则写出表中的①②③④⑤填的数据;
(2)作出频率分布直方图;
(3)试估计参加这次竞赛的学生的平均成绩
(本小题满分10分)
在某中学举行的物理知识竞赛中,将三个年级参赛学生的成绩再进行整理后分成5组,绘制出如图所示的频率分布直方图,图中从左到右依次为第一、第二、第三、第四、第五小组,已知第三小组的频数是15.
(1) 求成绩在50-70分的频率是多少?
(2) 求这三个年级参赛学生的总人数是多少?
(3) 求成绩在80-100分的学生人数是多少?