如图,在四棱锥A-BCDE中,侧面∆ADE是等边三角形,底面BCDE是等腰梯形,且CD∥BE,DE=2,CD=4, ,M是DE的中点,F是AC的中点,且AC=4,
,M是DE的中点,F是AC的中点,且AC=4,
求证:(1)平面ADE⊥平面BCD;
(2)FB∥平面ADE.
如图,在四棱锥A-BCDE中,底面四边形BCDE是等腰梯形,BC∥DE, =45
=45 ,O是BC的中点,AO=
,O是BC的中点,AO= ,且BC=6,AD=AE=2CD=2
,且BC=6,AD=AE=2CD=2 ,
,
(1)证明:AO⊥平面BCD;(2)求二面角A-CD-B的平面角的正切值.
如图,三棱锥 中,
中, ,
,

(Ⅰ)求证: ;
;
(Ⅱ)若 ,
, 是
是 的中点,求
的中点,求 与平面
与平面 所成角的正切值
所成角的正切值
如图,在等腰梯形 中,
中, 是梯形的高,
是梯形的高, ,
, ,现将梯形沿
,现将梯形沿 折起,使
折起,使 ,且
,且 ,得一简单组合体
,得一简单组合体 如图所示,已知
如图所示,已知 分别为
分别为 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求证: 平面
平面 .
.
如图,四棱锥 的底面是直角梯形,
的底面是直角梯形, ,
, ,
, 和
和 是两个边长为
是两个边长为 的正三角形,
的正三角形, ,
, 为
为 的中点,
的中点, 为
为 的中点.
的中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
如图,正三棱柱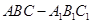 中,点
中,点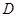 是
是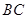 的中点.
的中点.
(Ⅰ)求证: 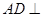 平面
平面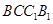 ;
;
(Ⅱ)求证: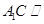 平面
平面 .
.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形, ,
,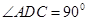 ,平面
,平面 底面
底面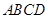 ,
, 为
为 中点,M是棱PC上的点,
中点,M是棱PC上的点,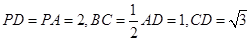 .
.
(1)若点M是棱PC的中点,求证: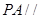 平面
平面 ;
;
(2)求证:平面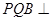 底面
底面 ;
;
(3)若二面角M-BQ-C为 ,设PM=tMC,试确定t的值.
,设PM=tMC,试确定t的值.
下面四个命题:
①“直线a∥直线b”的充要条件是“a平行于b所在的平面”;
②“直线 ⊥平面
⊥平面 内所有直线”的充要条件是“
内所有直线”的充要条件是“ ⊥平面
⊥平面 ”;
”;
③“直线a、b为异面直线”的充分不必要条件是“直线a、b不相交”;
④“平面 ∥平面
∥平面 ”的必要不充分条件是“
”的必要不充分条件是“ 内存在不共线三点到
内存在不共线三点到 的距离相等”;
的距离相等”;
其中正确命题的序号是
| A.①② | B.②③ | C.③④ | D.②④ |
已知 是直线,
是直线,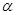 是平面,
是平面, 、
、
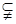
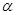 ,则“
,则“ 平面
平面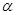 ”是“
”是“ 且
且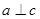 ”的 ………………………………………………………………………… ( )
”的 ………………………………………………………………………… ( )
| A.充要条件. | B.充分非必要条件. | C.必要非充分条件. | D.非充分非必要条件 |
如右图,E、F分别是正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是 .(要求:把可能的图的序号都填上)
如右图,E、F分别是正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是 .(要求:把可能的图的序号都填上)
圆锥的轴截面SAB是边长为2的等边三角形,O为底面中心,M为SO的中点,动点P在圆锥底面内(包括圆周)。若AM⊥MP,则P点形成的轨迹的长度为( )
A. |
B. |
C. 3 | D. |