设 为两条不同的直线,
为两条不同的直线, 为两个不同的平面.下列命题中,正确的是( )
为两个不同的平面.下列命题中,正确的是( )
A.若 与 与 所成的角相等,则 所成的角相等,则 |
B.若 , , ,则 ,则 |
C.若 , , ,则 ,则 |
D.若 , , ,则 ,则 |
(本小题满分14分)如图所示,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,M、N分别是AB、PC的中点,PA=AD=a.
(1)求证:MN∥平面PAD;
(2)求证:平面PMC⊥平面PCD.
(本小题满分12分)如图,在四棱锥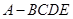 中,底面
中,底面 为矩形,侧面
为矩形,侧面 底面
底面 ,
,
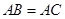 .
.
(1)求证: 面
面 ;
;
(2)设 为等边三角形,求直线
为等边三角形,求直线 与平面
与平面 所成角的大小.
所成角的大小.
若 、
、 、
、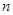 是互不相同的空间直线,α、β是不重合的平面,则下列结论正确的是
是互不相同的空间直线,α、β是不重合的平面,则下列结论正确的是
A.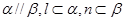   |
B.   |
C.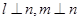   |
D.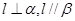   |
(本小题满分12分)如图1,在直角梯形 中,
中,
 ,
, ,点
,点 为线段
为线段 的中点,将
的中点,将 沿
沿 折起,使平面
折起,使平面 平面
平面 ,得到几何体
,得到几何体 ,如图2所示.
,如图2所示.
(Ⅰ)求证: 平面
平面 ;
;
【理】(Ⅱ)求二面角 的余弦值.
的余弦值.
【文】(Ⅱ)求点 到平面
到平面 的距离.
的距离.
(本小题12分)如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.

(1)求证:AC⊥平面BDE;
(2)求二面角FBED的余弦值.
(本小题满分12分)在三棱锥M-ABC中,AB=2AC=2,MA=MB= ,AB=4AN,AB^AC,平面MAB^平面ABC,S为BC的中点.
,AB=4AN,AB^AC,平面MAB^平面ABC,S为BC的中点.
(1)证明:CM^SN;
(2)求SN与平面CMN所成角的大小.
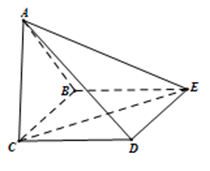
(本小题满分16分)在四棱锥 中,
中, 平面
平面 ,
, 是正三角形,
是正三角形, 与
与 的交点
的交点 恰好是
恰好是 中点,又
中点,又 ,
, ,点
,点 在线段
在线段 上,且
上,且 .
.
(1)求证: ;
;
(2)求证: ∥平面
∥平面 ;
;
(3)求二面角 的余弦值.
的余弦值.
(本小题满分13分)
如图,在四棱锥 中,底面
中,底面 四边长为1的菱形,
四边长为1的菱形, ,
,  ,
,  ,
, 为
为 的中点,
的中点, 为
为 的中点
的中点
(Ⅰ)证明:直线
 ;
;
(Ⅱ)求异面直线AB与MD所成角的大小;
(Ⅲ)求点B到平面OCD的距离。