(本小题满分14分)如图,在斜三棱柱 中,侧面
中,侧面 是边长为
是边长为 的菱形,
的菱形, .在面
.在面 中,
中, ,
, ,
, 为
为 的中点,过
的中点,过 三点的平面交
三点的平面交 于点
于点 .
.
(1)求证: 为
为 中点;
中点;
(2)求证:平面 平面
平面 .
.
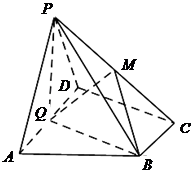
(本小题满分14分)如图,在四棱锥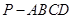 中,底面
中,底面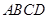 为直角梯形,
为直角梯形,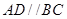 ,
,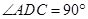 ,平面
,平面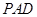 ⊥底面
⊥底面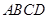 ,
,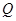 为
为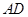 的中点,
的中点,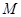 是棱
是棱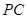 上的点,
上的点,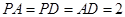 ,
,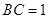 ,
,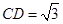 .
.
(1)求证:平面 ⊥平面
⊥平面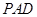 ;
;
(2)若二面角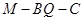 为
为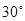 ,设
,设 ,试确定
,试确定 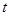 的值.
的值.
已知 是三条不同的直线,命题:“
是三条不同的直线,命题:“ ∥
∥ 且
且 ”是真命题,如果把
”是真命题,如果把 中的两条直线换成两个平面,在所得3个命题中,真命题的个数为( )
中的两条直线换成两个平面,在所得3个命题中,真命题的个数为( )
A. |
B. |
C.2 | D.3 |
(本小题满分12分)如图,在菱形 中,
中, ,
, ,
,  分别是边
分别是边 ,
, 的中点,
的中点, ,沿
,沿 将△
将△ 翻折到△
翻折到△ ,连接
,连接 ,得到如图的五棱锥
,得到如图的五棱锥 .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)若 ,求二面角
,求二面角 的大小.
的大小.
(本小题满分12分)如图四棱锥 ,
, ,
, ,
, 平面
平面 ,
, ,M为
,M为 的中点.
的中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)在平面 上找一点N,使得
上找一点N,使得 平面
平面 ;
;
(Ⅲ)求直线 与平面
与平面 所成角的正弦.
所成角的正弦.
如图,在三棱锥 中,
中, 平面
平面 ,
, ,
, ,
, 、
、 、
、 分别为
分别为 、
、 、
、 的中点,
的中点, 、
、 分别为线段
分别为线段 、
、 上的动点,且有
上的动点,且有 .
.
(1)求证: 面
面 ;
;
(2)探究:是否存在这样的动点M,使得二面角 为直二面角?若存在,求CM的长度;若不存在,说明理由.
为直二面角?若存在,求CM的长度;若不存在,说明理由.
(本小题满分12分)如图, 是正方形,
是正方形, 平面
平面 .
.
(1)求证: 平面
平面 ;
;
(2)若 ,
, ,点
,点 在线段
在线段 上,且
上,且 ,求证:
,求证: 平面
平面 .
.
 是矩形,
是矩形, ,
, ,沿
,沿 将
将 折起到
折起到 ,使平面
,使平面 平面
平面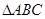 ,
, 是
是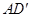 的中点,
的中点, 是
是 上的一点,给出下列结论:
上的一点,给出下列结论:
① 存在点 ,使得
,使得 平面
平面
② 存在点 ,使得
,使得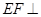 平面
平面
③ 存在点 ,使得
,使得 平面
平面
④ 存在点 ,使得
,使得 平面
平面
其中正确结论的序号是 .(写出所有正确结论的序号)
如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB=BC=2, AD=CD= ,PA=
,PA= ,∠ABC=120°,G为线段PC上的点
,∠ABC=120°,G为线段PC上的点
(Ⅰ)证明:BD⊥面PAC
(Ⅱ)若G是PC的中点,求DG与APC所成的角的正切值
(Ⅲ)若G满足PC⊥面BGD,求 的值.
的值.
(本小题满分14分)已知三棱锥 中,
中, 平面
平面 ,
, ,
, 为
为 中点,
中点, 为
为 的中点,
的中点,
(1)求证: 平面
平面 ;
;
(2)求证:平面 平面
平面 .
.