如图,四棱锥 的底面是正方形,
的底面是正方形,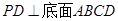 ,点
,点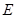 在棱
在棱 上
上
(1)求证:平面 平面
平面 ;
;
(2)当 ,且
,且 时,确定点
时,确定点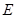 的位置,即求出
的位置,即求出 的值
的值
(本小题满分15分)如图甲, 是边长为6的等边三角形,
是边长为6的等边三角形, ,
, 分别为
分别为 、
、 靠近
靠近 、
、 的三等分点,点
的三等分点,点 为
为 边的中点.线段
边的中点.线段 交线段
交线段 于
于 点,将
点,将 沿
沿 翻折,使平面
翻折,使平面 ⊥平面
⊥平面 ,连接
,连接 、
、 、
、 形成如图乙所示的几何体.
形成如图乙所示的几何体.
(Ⅰ)求证 ⊥平面
⊥平面 ;
;
(Ⅱ)求二面角 的余弦值.
的余弦值.
设 ,
, 是两条不同的直线,
是两条不同的直线, ,
, 是两个不同的平面,下列命题中正确的是( )
是两个不同的平面,下列命题中正确的是( )
A.若 则 则 |
B.若 则 则 |
C.若 则 则 |
D.若 则 则 |
如图,一简单几何体的一个面 内接于圆
内接于圆 ,
, 分别是
分别是 的中点,
的中点, 是圆
是圆 的直径,四边形
的直径,四边形 为平行四边形,且
为平行四边形,且 平面
平面 .
.
(1)求证: 平面
平面 ;
;
(2)若AC=BC=BE=2,求二面角O-CE-B的余弦值.
在如图所示的几何体中,四边形 是等腰梯形,
是等腰梯形, ∥
∥ ,
, ,
, .在梯形
.在梯形 中,
中, ∥
∥ ,且
,且 ,
, ⊥平面
⊥平面 .
.
(Ⅰ)求证: ;
;
(Ⅱ)若二面角 为
为 ,求
,求 的长.
的长.
下列命题错误的是( )
A.如果平面 平面 平面 ,那么平面 ,那么平面 内一定存在直线平行于平面 内一定存在直线平行于平面 |
B.如果平面 平面 平面 ,那么平面 ,那么平面 内所有直线都垂直于平面 内所有直线都垂直于平面 |
C.如果平面 平面 平面 ,平面 ,平面 平面 平面 , , 那么 那么 平面 平面 |
D.如果平面 不垂直于平面 不垂直于平面 ,那么平面 ,那么平面 内一定不存在直线垂直于平面 内一定不存在直线垂直于平面 |
已知直线 ,直线
,直线 ,给出下列命题:①
,给出下列命题:① ∥
∥ ; ②
; ② ∥m; ③
∥m; ③ ∥
∥ ;④
;④ ∥
∥ ;其中正确命题的序号是( )
;其中正确命题的序号是( )
| A.①②③ | B.②③④ | C.①③ | D.②④ |
(本小题满分12分)如图,在四棱锥 中,
中, ,
, ,
, ,
, ,平面
,平面 平面
平面 .
.
(Ⅰ)求证:平面 平面
平面 ;
;
(Ⅱ)若直线 与平面
与平面 所成的角的正弦值为
所成的角的正弦值为 ,求二面角
,求二面角 的余弦值.
的余弦值.
已知直线 平面
平面 ,直线
,直线 平面
平面 ,有下列四个命题:
,有下列四个命题:
①若 ,则
,则 ;
;
②若 ,则
,则 ;
;
③若 ,则
,则 ;
;
④若 ,则
,则 .
.
以上命题中,正确命题的序号是( )
| A.①② | B.①③ | C.②④ | D.③④ |
空间中,对于平面 和共面的两直线
和共面的两直线 、
、 ,下列命题中为真命题的是( )
,下列命题中为真命题的是( )
A.若 , , ,则 ,则 |
B.若 , , ,则 ,则 |
C.若 、 、 与 与 所成的角相等,则 所成的角相等,则 |
D.若 , , ,则 ,则 |
(本小题满分13分,(1)小问6分,(2)小问7分)
如图,在四棱锥 中,底面为直角梯形,
中,底面为直角梯形, ,
, ,
, 底面
底面 ,且
,且 ,
, 、
、 分别为
分别为 、
、 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求证: .
.
(本小题满分12分)如图,在斜三棱柱 中,O是AC的中点,A1O⊥平面
中,O是AC的中点,A1O⊥平面 ,
,  ,
, .
.
(1)求证: AC1⊥平面A1BC;
(2)若AA1=2,求点C到平面 的距离。
的距离。
(本小题满分14分)在四棱锥 中,
中, 平面
平面 ,
, 是边长为4的正三角形,
是边长为4的正三角形, 与
与 的交点
的交点 恰好是
恰好是 中点,又
中点,又 ,点
,点 在线段
在线段 上,且
上,且 .
.
(1)求证: ;
;
(2)求证: 平面
平面 .
.