高中数学立体图形的结构特征选择题

不共面的四个定点到平面α的距离都相等，这样的平面α共有（　　）

A．3个

B．4个

C．6个

D．7个

已知正四棱柱ABCD﹣A₁B₁C₁D₁中，AA₁=2AB，E为AA₁中点，则异面直线BE与CD₁所成角的余弦值为（　　）

A．

B．

C．

D．

已知下列三个命题：
①若一个球的半径缩小到原来的，则其体积缩小到原来的；
②若两组数据的平均数相等，则它们的标准差也相等；
③直线x+y+1=0与圆相切．
其中真命题的序号是（　　）

A．①②③

B．①②

C．①③

D．②③

已知三棱锥中，，，，，，则关于该三棱锥的下列叙述正确的为（）

A．表面积	B．表面积为
C．体积为	D．体积为

已知三棱锥中，，，，，，则三棱锥的外接球的表面积为（）

A．

B．

C．

D．

如图，正方体中，点为线段上一动点，点为底面内（含边界）一动点，为的中点，点构成的点集是一个空间几何体，则该几何体为（）

A．棱柱	B．棱锥
C．棱台	D．球

某四棱锥的三视图如图所示，则最长的一条侧棱长度为（）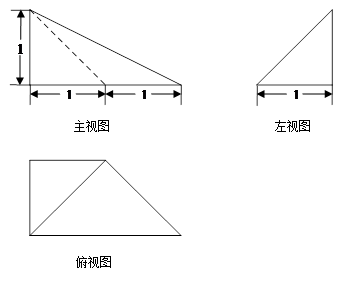

A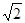．	B．
C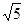．	D．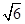

将正三棱柱截去三个角（如图（1）所示A、B、C分别是△GHI三边的中点）得到几何体如图（2），则该几何体按图（2）所示方向的侧视图（或称左视图）为（）


A B C D

已知下列三个命题：
①若一个球的半径缩小到原来的，则其体积缩小到原来的；
②若两组数据的平均数相等，则它们的标准差也相等；
③直线x＋y＋1＝0与圆x²＋y²＝相切．
其中真命题的序号是(　　)

A．①②③	B．①②
C．①③	D．②③

球面上有3个点，其中任意两点的球面距离都等于大圆周长的，经过3个点的小圆的周长为，那么这个球的半径为（　　）

A．

B．

C．2

D．

已知地球的半径为，球面上两点都在北纬45°圈上，它们的球面距离为，点在东经30°上，则两点所在其纬线圈上所对应的劣弧的长度为（）

A．

B．

C．

D．

、是半径为的球的球面上两点，它们的球面距离为，求过、的平面中，与球心的最大距离是（）

A．

B．

C．

D．

已知A，B两地都位于北纬45°，又分别位于东经30°和60°，设地球半径为R，则A，B的球面距离约为 ( )

A．

B．

C．

D．

设地球半径为R，则东经线上，纬度分别为北纬和的两地A，B的球面距离为( )

A．

B．

C．

D．

平面α截球O的球面所得圆的半径为1，球心O到平面α的距离为，则此球的体积为(　　)

A．

B．

C．

D．