已知球的两个平行截面的面积分别为5π和8π,它们位于球心的同一侧且相距是1,那么这个球的半径是 ( )
| A.4 | B.3 | C.2 | D.5 |
我们把底面是正三角形,顶点在底面的射影是正三角形中心的三棱锥称为正三棱锥。现有一正三棱锥 放置在平面
放置在平面 上,已知它的底面边长为2,高为
上,已知它的底面边长为2,高为 ,
, 在平面
在平面 上,现让它绕
上,现让它绕 转动,并使它在某一时刻在平面
转动,并使它在某一时刻在平面 上的射影是等腰直角三角形,则
上的射影是等腰直角三角形,则 的取值范围是().
的取值范围是().
A. |
B. |
C.   . . |
D. |

球O为边长为2的正方体ABCD-A1B1C1D1的内切球,P为球O的球面上动点,M为B1C1中点, ,则点P的轨迹周长为( ).
,则点P的轨迹周长为( ).
A. |
B. |
C. |
D. |
正四棱锥S-ABCD的底面边长为4 ,高SE=8,则过点A,B,C,D,S的球的半径为( )
,高SE=8,则过点A,B,C,D,S的球的半径为( )
| A.3 | B.4 | C.5 | D.6 |
已知底面边长为1,侧棱长为 的正四棱柱的各顶点均在同一个球面上,则该球的体积为()
| A. | B. | C. | D. |
如右图,在长方体 中, ,一质点从顶点 射向点 ,遇长方体的面反射(反射服从光的反射原理),将 次到第 次反射点之间的线段记为 , ,将线段 竖直放置在同一水平线上,则大致的图形是()





A B C D
[2013·北京高考]如图,在正方体ABCD-A1B1C1D1中,P为对角线BD1的三等分点,P到各顶点的距离的不同取值有( )
| A.3个 | B.4个 | C.5个 | D.6个 |
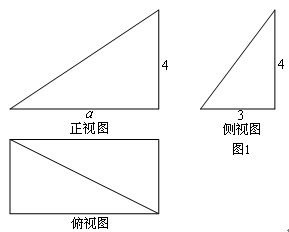
已知某几何体的三视图如图所示,若该几何体的体积为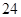 ,则正视图中
,则正视图中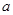 的值为()
的值为()
A.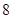 |
B.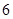 |
C.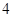 |
D.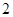 |
一平面截一球得到直径为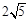 cm的圆面,球心到这个平面的距离是2 cm,则该球的体积是()
cm的圆面,球心到这个平面的距离是2 cm,则该球的体积是()
| A.12 cm3 | B.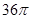 cm3 cm3 |
C. cm3 cm3 |
D.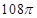 cm3 cm3 |
已知圆锥的底面半径为R,高为3R,在它的所有内接圆柱中,全面积的最大值是( )
| A.22πR2 | B. πR2 πR2 |
C. πR2 πR2 |
D. πR2 πR2 |
已知一个三棱柱,其底面是正三角形,且侧棱与底面垂直,一个体积为 的球体与棱柱的所有面均相切,那么这个三棱柱的表面积是( )
的球体与棱柱的所有面均相切,那么这个三棱柱的表面积是( )
A. |
B. |
C. |
D. |
设△ABC的三边长分别为a、b、c,△ABC的面积为S,内切圆半径为r,则r= ;类比这个结论可知:四面体S-ABC的四个面的面积分别为S1、S2、S3、S4,内切球的半径为r,四面体S-ABC的体积为V,则r=( )
;类比这个结论可知:四面体S-ABC的四个面的面积分别为S1、S2、S3、S4,内切球的半径为r,四面体S-ABC的体积为V,则r=( )
A. |
B. |
C. |
D. |