高中数学立体图形的结构特征选择题

如图，在一个正方体内放入两个半径不相等的球，这两个球相外切，且球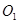与正方体共顶点A的三个面相切，球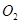与正方体共顶点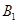的三个面相切,则两球在正方体的面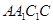上的正投影是（）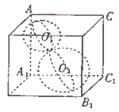

已知矩形ABCD的面积为8，当矩形ABCD周长最小时，沿对角线AC把
△ACD折起，则三棱锥D－ABC外接的球表面积等于(　　)．

A．8π

B．16π

C．48π

D．不确定的实数

如图，正方体的底面与正四面体的底面在同一平面α上，且AB∥CD，正方体的六个面所在的平面与直线CE，EF相交的平面个数分别记为m，n，那么m＋n等于(　　)．

A．8

B．9

C．10

D．11

如图，正方体的棱长为，以顶点A为球心，2为半径作一个球，则图中球面与正方体的表面相交所得到的两段弧长之和等于( )

A．

B．

C．

D．

半径为 $R$的球 $O$的直径 $AB$垂直于平面 $\alpha$，垂足为 $B$， $△BCD$是平面 $\alpha$内边长为 $R$的正三角形，线段 $AC,AD$分别与球面交于点 $M,N$，那么 $M,N$两点间的球面距离是（）

A．	$Rarc\cos \frac{17}{25}$	B．	$Rarc\cos \frac{18}{25}$
C．	$\frac{1}{3}\pi R$	D．	$\frac{4}{15}\pi R$

在正四棱锥S-ABCD中，侧面与底面所成的角为，则它的外接球半径R与内切球半径之比为（　）

A．5

B．

C．10

D．

已知三棱柱ABC－A₁B₁C₁的侧棱与底面垂直，体积为，底面是边长为的正三角形．若P为底面A₁B₁C₁的中心，则PA与平面ABC所成角的大小为 (　　)．

A．

B．

C．

D．

在正四棱锥S-ABCD中，侧面与底面所成的角为，则它的外接球半径R与内切球半径之比为（　）

A．5

B．

C．10

D．

设△ABC的三边长分别为a、b、c，△ABC的面积为S，内切圆半径为r，则r＝；类比这个结论可知：四面体S－ABC的四个面的面积分别为S₁、S₂、S₃、S₄，内切球的半径为r，四面体S－ABC的体积为V，则r＝(　 　)

A．

B．

C．

D．

如右图，在长方体 $ABCD-A_1{B}_1{C}_1{D}_1$中， $AB=11,AD=7,A{A}_1=12$，一质点从顶点 $A$射向点 $E\left(4,3,12\right)$，遇长方体的面反射（反射服从光的反射原理），将 $i-1$次到第 $i$次反射点之间的线段记为 $L\left(i=2,3,4\right)$， $L_1=AE$，将线段 $L_1,L_2,L_3,L_4$竖直放置在同一水平线上，则大致的图形是（）

A B C D

长方体的一个顶点三条棱长分别为1，2，3，该长方体的顶点都在同一个球面上，则这个球的表面积为（s=4）（）

A．

B．14

C．56

D．96

如图，正四棱柱中，，，分别在上移动，且始终保持平面，设，，则函数的图象大致是

把四个半径都是1的球中的三个放在桌面上，使它两两外切，然后在它们上面放上第四个球，使它与前三个都相切，求第四个球的最高点与桌面的距离（）

A．

B．

C．

D．3

如图，是正方体对角线上一动点，设的长度为，若的面积为，则的图象大致是（）

如图，等边三角形的中线与中位线相交于，已知是△绕旋转过程中的一个图形，下列命题中，错误的是（）

A．动点在平面上的射影在线段上

B．恒有平面⊥平面

C．三棱锥的体积有最大值

D．异面直线与不可能垂直